Взаимодействующие равные: распределенное умножение матриц
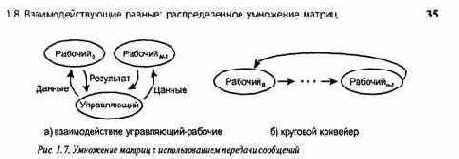
Ранее было показано, как реализовать параллельное умножение матриц с помощью процессов, разделяющих переменные. Здесь представлены два способа решения этой задачи с использованием процессов, взаимодействующих с помощью пересылки сообщений. Более сложные алгоритмы представлены в главе 9. Первая программа использует управляющий процесс и массив независимых рабочих процессов. Во второй программе рабочие процессы равны и их взаимодействие обеспечивается круговым конвейером. Рис. 1.7 иллюстрирует структуру схем взаимодействия этих процессов. Как показано в части 2, они часто встречаются в распределенных параллельных вычислениях.
На машинах с распределенной памятью каждый процессор имеет доступ только к собственной локальной памяти. Это значит, что программа не может использовать глобальные переменные, поэтому любая переменная должна быть локальной для некоторого процесса и может быть доступной только этому процессу или процедуре. Следовательно, для взаимодействия процессы должны использовать передачу сообщений.
Допустим, что нам необходимо получить произведение матриц а и Ь, а результат поместить в матрицу с. Предположим, что каждая из них имеет размер пхп и существует п процессоров. Можно использовать массив из п рабочих процессов, поместив по одному на каждый процессор и заставив каждый рабочий процесс вычислять одну строку результирующей матрицы с. Программа для рабочих процессов будет выглядеть следующим образом.
process worker[i = 0 to n-1] {
double a[n]; # строка i матрицы а double b[n,n]; # вся матрица b double c[n],- # строка i матрицы с receive начальные значения вектора а и матрицы Ъ; for [j = 0 to n-1] { c[j] = 0.0; for [k = 0 to n-1]
c[j] = c[j] + a[k] * b[k,j]; }
send вектор-результат с управляющему процессу; }
Рабочий процесс i вычисляет строку i результирующей матрицы с. Чтобы это сделать, он должен получить строку i исходной матрицы а и всю исходную матрицу Ь.
Каждый рабочий процесс сначала получает эти значения от отдельного управляющего процесса. Затем рабочий процесс вычисляет свою строку результатов и отсылает ее обратно управляющему. (Или, возможно, исходные матрицы являются результатом предшествующих вычислений, а результирующая — входом для последующих; это пример распределенного конвейера.)
Управляющий процесс инициирует вычисления, собирает и выводит их результаты. В частности, сначала управляющий процесс посылает каждому рабочему соответствующую строку матрицы а и всю матрицу Ь. Затем управляющий процесс ожидает получения строк матрицы с от каждого рабочего. Схема управляющего процесса такова.

36 Глава 1. Обзор области параллельных вычислений
receive строку i матрицы с от процесса worker [i],-вывести результат, который теперь в матрице с ;
}
Операторы send и receive, используемые управляющим процессом, — это примитивы (элементарные действия) передачи сообщений. Операция send упаковывает сообщение и пересылает его другому процессу; операция receive ожидает сообщение от другого процесса, а затем сохраняет его в локальных переменных. Подробно передача сообщений будет описана в главе 7 и использована в программировании многочисленных приложений в частях 2 и 3.
Как и ранее, предположим, что каждый рабочий процесс получает одну строку матрицы а и должен вычислить одну строку матрицы с. Однако теперь допустим, что у каждого процесса есть только один столбец, а не вся матрица Ь. Итак, в начальном состоянии рабочий процесс i имеет столбец i матрицы Ь. Имея лишь эти исходные данные, рабочий процесс может вычислить только значение с [ i, i ]. Для того чтобы рабочий процесс i мог вычислить всю строку матрицы с, он должен получить все столбцы матрицы Ь. Для этого можно использовать круговой конвейер (см. рис. 1.7,б), в котором по рабочим процессам циркулируют, столбцы. Каждый рабочий процесс выполняет последовательность раундов; в каждом раунде ' он отсылает свой столбец матрицы Ь следующему процессу и получает другой ее столбец от предыдущего.
Программа имеет следующий вид.

В данной программе рабочие процессы упорядочены в соответствии с их индексами. (Для процесса п-1 следующим является процесс 0, а предыдущим для 0 — п-1.) Столбцы матрицы Ь передаются по кругу между рабочими процессами, поэтому каждый процесс в конце концов получит каждый столбец. Переменная nextCol отслеживает, куда в векторе с поместить очередное промежуточное произведение. Как и в первом вычислении, предполагается, что управляющий процесс отправляет строки матрицы а и столбцы матрицы Ь рабочим, а затем получает от них строки матрицы с.
1 9. Обзор программной нотации 37
Во второй программе использовано отношение между процессорами, которое называется взаимодействующие равные (interacting peers), или просто равные. Каждый рабочий процесс выполняет один и тот же алгоритм и взаимодействует с другими рабочими, чтобы вычислить свою часть необходимого результата. Дальнейшие примеры взаимодействующих равных мы увидим в частях 2 и 3. В одних случаях, как и здесь, каждый из рабочих процессов общается только с двумя своими соседями, в других — каждый из рабочих взаимодействует со всеми остальными процессами.
В первой из приведенных выше программ значения из матрицы Ь дублируются в каждом рабочем процессе. Во второй программе в любой момент времени у каждого процесса есть одна строка матрицы а и только один столбец матрицы Ь. Это снижает затраты памяти для каждого процесса, но вторая программа выполняется дольше первой, поскольку на каждой ее итерации каждый рабочий процесс должен отослать сообщение одному соседу и получить сообщение от другого. Данные программы иллюстрируют классическое противоречие между временем и пространством в вычислениях. В разделе 9.3 представлены другие алгоритмы для распределенного умножения матриц, иллюстрирующие дополнительные противоречия между временем и пространством.