Управляющий-рабочие (распределенный портфель задач)
В разделе 3.6 представлена парадигма портфеля задач и показано, как реализовать ее, используя для синхронизации и взаимодействия разделяемые переменные. Напомним основную идею: несколько рабочих процессов совместно используют портфель независимых задач. Рабочий многократно берет из портфеля задачу, выполняет ее и, возможно, порождает одну или несколько новых задач, помещая их в портфель. Преимуществами этого подхода к реализации параллельных вычислений являются легкость варьирования числа рабочих процессов и относительная простота обеспечения того, что процессы выполняют приблизительно одинаковые объемы работы.
Глава 9. Модели взаимодействия процессов 329
Здесь показано, как реализовать парадигму портфеля задач с помощью передачи сообщений вместо разделяемых переменных. Для этого портфель задач реализуется управляющим процессом, который выбирает задачи, собирает результаты и определяет завершение работы. Рабочие процессы получают задачи и возвращают результаты, взаимодействуя с управляющим, который, по сути, является сервером, а рабочие процессы — клиентами.
В первом примере, приведенном ниже, показано, как умножаются разреженные матрицы (большинство их элементов равны нулю). Во втором примере используется сочетание интервалов статического и адаптивного интегрирования в уже знакомой задаче квадратуры. В обоих примерах общее число задач фиксировано, а объем работы, выполняемой каждой задачей, изменяется.
9.1.1. Умножение разреженных матриц
Пусть А и В — матрицы размером n x п. Нужно определить произведение матриц А х в = С. Для этого необходимо вычислить п2 скалярных произведений векторов (сумм, образованных произведениями соответствующих элементов двух векторов длины п).
Матрица называется плотной, если большинство ее элементов не равны нулю, ч разреженной, если большинство элементов нулевые. Если А и в — плотные матрицы, то матрица с тоже будет плотной (если только в скалярных произведениях не произойдет значительного сокращения).
С другой стороны, если А или в — разреженные матрицы, то с тоже будет разреженной, поскольку каждый нуль в А или в даст нулевой вклад в n скалярных произведений. Например, если в строке матрицы А есть только нули, то и вся соответствующая строка с будет состоять из нулей.
Разреженные матрицы возникают во многих задачах, например, при численной аппроксимации решений дифференциальных уравнений в частных производных или в больших системах линейных уравнений. Примером разреженной матрицы является трехдиагональная матрица, у которой равны нулю все элементы, кроме главной диагонали и двух диагоналей непосредственно над и под ней. Если известно, что матрицы разреженные, то запоминание только ненулевых элементов экономит память, а игнорирование нулевых элементов при умножении уменьшает затраты времени.
Разреженная матрица А представляется информацией о ее строках:
int lengthA[n]; pair *elementsA[n];
Значение lengthAfi] является числом ненулевых элементов в строке i матрицы А. Переменная elementsAfi] указывает на список ненулевых элементов строки 1. Каждый элемент представлен парой значений (записью): целочисленным индексом столбца и значением соответствующего элемента матрицы (числом удвоенной точности). Таким образом, если значение lengthAfi] равно 3, то в списке elementsAfi] есть три пары. Они упорядочены по возрастанию индексов столбцов. Рассмотрим конкретный пример. lengthA elementsA
1 (3, 2.5) О
О
2 (1, -1.5) (4, 0.6) О
1 (0, 3.4)
Здесь записана матрица размерами 6 на б, в которой есть четыре ненулевых элемента: в строке 0 и столбце 3, в строке 3 и столбце 1, в строке 3 и столбце 4, в строке 5 и столбце 0.
Матрицу с представим так же, как и А. Чтобы упростить умножение, представим матрицу в не строками, а столбцами. Тогда значения в lengths будут указывать число ненулевых элементов в каждом столбце матрицы в, а в elementsB — храниться пары вида (номер строки, значение элемента).
330 Часть 2. Распределенное программирование
Для вычисления произведения матриц а и в, как обычно, нужно просмотреть п2 пар строк и столбцов. Для разреженных матриц самый подходящий объем задачи соответствует одной строке результирующей матрицы с, поскольку вся эта строка представляется одним вектором пар (столбец, значение). Таким образом, нужно столько задач, сколько строк в матрице А. (Очевидно, что для оптимизации можно пропускать строки матрицы А, полностью состоящие из нулей, т.е. строки, для которых lengthA [ i ] равно 0, поскольку соответствующие строки матрицы С тоже будут нулевыми. Но в реальных задачах это встречается редко.)
В листинге 9.1 показан код, реализующий умножение разреженных матриц с помощью одного управляющего и нескольких рабочих процессов. Предполагается, что матрица А в управляющем процессе уже инициализирована, а у каждого рабочего есть инициализированная копия матрицы в. Процессы взаимодействуют с помощью примитивов рандеву (см. главу 8), что упрощает программу. Для использования асинхронной передачи сообщений управляющий процесс должен быть запрограммирован в стиле активного монитора (см. раздел 7.3), а вызовы call в рабочих процессах нужно заменить вызовами send и receive.


332 Часть 2. Распределенное программирование
фала функции f (х) на интервале от а до Ь. В разделе 3.6 было показано, как реализовать адаптивную квадратуру с помощью разделяемого портфеля задач.
Здесь для реализации распределенного портфеля задач используется управляющий процесс. Но вместо "чистого" алгоритма адаптивной квадратуры, использованного в листинге 3.18, применяется комбинация статического и динамического алгоритмов. Интервал от а до Ь делится на фиксированное число подынтервалов, и для каждого из них используется алгоритм адаптивной квадратуры. Такое решение сочетает простоту итерационного алгоритма и высокую точность адаптивного.
Использование фиксированного числа задач упрощает программы управляющего и рабочих процессов, а также уменьшает число взаимодействий между ними.
В листинге 9.2 приведен код управляющего и рабочих процессов. Поскольку управляющий процесс, по существу, является серверным, для его взаимодействия с рабочими процессами здесь также используются рандеву. Таким образом, управляющий процесс имеет ту же структуру, что и в листинге 9.1, а, и также экспортирует операции getTask и putResult, но параметры операций отличаются. Теперь задача определяется конечными точками интервала (переменные left и right), а результатом вычислений является площадь под графиком f (х) на этом интервале. Предполагается, что значения переменных а, Ь и numlntervals заданы, например, как аргументы командной строки. По этим значениям управляющий процесс вычисляет ширину интервалов. Затем он выполняет цикл, принимая вызовы операций getTask и putTask, пока не получит по одному результату вычислений для каждого интервала (каждой задачи). Отметим использование условия синхронизации "st x< Ь" в ветви ••для операции getTask оператора ввода— оно предохраняет операцию getTask от выдачи следующей задачи, когда портфель задач уже пуст.
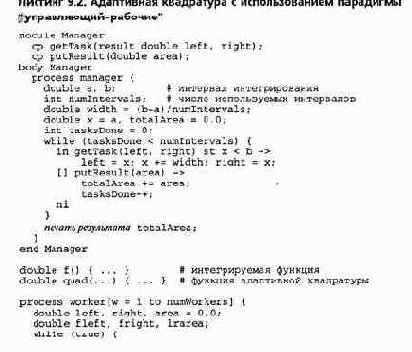

Рабочие процессы в листинге 9.2 разделяют или имеют собственные копии кода функций f и quad (рекурсивная функция quad приведена в разделе 1.5). Рабочий процесс циклически получает задачу от управляющего, вычисляет необходимые для функции quad аргументы, вызывает ее для аппроксимации значения площади под графиком функции от f (left) до f (right), а затем отсылает результат управляющему процессу.
Когда программа в листинге 9.2 завершается, рабочие процессы блокируются в своих вызовах функции getTask. Обычно это безопасно, как и здесь, но в некоторых случаях этот способ завершения выполнения рабочих процессов может привести к зависанию. Задача реализации нормального завершения рабочих процессов оставляется читателю. (Указание. Измените функцию getTask, чтобы она возвращала true или false.)
В рассматриваемой программе объем работы, приходящейся на одну задачу, зависит от скорости изменения функции f. Таким образом, если число задач приблизительно равно числу рабочих процессов, то вычислительная нагрузка почти наверняка будет несбалансированной. С другой стороны, если задач слишком много, то между управляющим и рабочими процессами будут происходить ненужные взаимодействия, что приведет к излишним накладным расходам. Было бы идеально иметь такое число задач, при котором общий объем работы приблизительно одинаков для всех рабочих процессов. Разумным является число задач, которое в два-три раза больше, чем число рабочих процессов (в данной программе значение пи-mlntervals должно быть в два-три раза больше значения numWorkers).