Техника устранения взаимного вмешательства
Процессы в параллельной программе работают вместе над вычислением результата. Ключевое требование для получения правильной программы состоит в том, что процессы не должны влиять друг на друга. Совокупность процессов свободна от взаимного влияния, когда в одном процессе нет действий присваивания, вмешивающихся в критические утверждения другого процесса.
В данном разделе описаны четыре основных метода устранения взаимного вмешательства, которые можно использовать для разработки правильных параллельных программ: непересекающиеся множества переменных, ослабленные утверждения, глобальные инварианты и синхронизация. Эти методы широко применяются в оставшейся части книги. Все они включают запись утверждений и действий присваивания в форме, обеспечивающей истинность формулам (2.5).
2.7.1. Непересекающиеся множества переменных
Напомним, что множество записи процесса — это множество переменных, которым он присваивает значения (и, возможно, считывает их), а множество чтения процесса — это множество переменных, которые процесс считывает, но не изменяет. Множество ссылок процесса — это множество переменных, которые встречаются в утверждениях доказательства корректности данного процесса. Множество ссылок процесса часто (но не всегда) будет совпадать с объединением множеств чтения и записи. По отношению к взаимному вмешательству критические переменные — это переменные в утверждениях.
Если множество записи одного процесса не пересекается со множеством ссылок другого процесса и наоборот, то эти два процесса не могут влиять друг на друга. Формально это происходит потому, что в аксиоме присваивания используется текстуальная подстановка, которая не влияет на предикат, не содержащий ссылок на целевую переменную присваивания. (Локальные переменные в различных процессах, даже если и имеют одинаковые имена, все равно являются разными переменными; поэтому перед применением аксиомы присваивания их можно переименовать.)
В качестве примера рассмотрим следующую программу.
Другие процессы добавляют операции в очередь. Когда диск незанят, планировщик проверяет очередь, выбирает по некоторому критерию наилучшую операцию и начинает ее выполнять. В действительности диск не всегда будет выполнять наилучшую операцию, даже если она была таковой во время просмотра очереди. Это происходит потому, что процесс может добавить еще одну, лучшую, операцию в очередь сразу после того, как был сделан выбор, и даже до того, как диск начал выполнение операции. Таким образом, "наилучшая" в данном случае — это свойство, зависящее от времени, хотя для задачи планирования вроде приведенной этого достаточно.
Еще один пример — многие параллельные алгоритмы приближенного решения дифференциальных уравнений имеют следующий вид. (Более конкретный пример приводится в главе 11.) Пространство задачи аппроксимируется конечной сеткой точек, скажем, grid[n,n]. Каждой точке или (что типичнее) блоку точек сетки назначается процесс, как в следующем фрагменте программы.
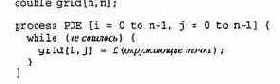
Глава 2 Процессы и синхронизация
Функция f, вычисляемая на каждой итерации, может быть, например, усреднением значений в четырех соседних точках той же строки и того же столбца. Во многих задачах значение, присваиваемое элементу grid [ i, j ] на одной итерации, зависит от значений соседних элементов на предыдущей. Таким образом, инвариант цикла должен характеризовать отношения между старыми и новыми значениями точек сетки.
Чтобы гарантировать, что инвариант цикла в каждом процессе не подвержен влиянию извне, процессы должны использовать две матрицы и после каждой итерации синхронизироваться. На каждой итерации каждый процесс pde считывает значения из матрицы, вычисляет f, а затем записывает результат во вторую матрицу. Потом он ждет, пока остальные процессы вычислят новые значения для своих точек сетки. (В следующей главе показано, как реализовать этот тип синхронизации, называемый барьером.) Затем роли матриц меняются местами, и процессы выполняют следующую итерацию.
Второй способ синхронизации процессов состоит в их пошаговом выполнении, когда все процессы одновременно выполняют одни и те же действия. Этот тип синхронизации поддерживается в синхронных процессорах. Данный метод позволяет избежать взаимного вмешательства, поскольку каждый процесс считывает старые значения из массива grid до того, как какой-либо из процессов присвоит новое значение.
2.7.3. Глобальные инварианты
Еще один, очень эффективный способ избежать взаимного вмешательства состоит в использовании глобального инварианта для учета всех отношений между разделяемыми переменными. Как показано в начале главы 3, глобальный инвариант можно использовать при разработке решения любой задачи синхронизации.
Предположим, что I — предикат, который ссылается на глобальные переменные. Тогда I называется глобальным инвариантом по отношению ко множеству процессов, если: 1) I истинен в начале выполнения процессов, 2) I сохраняется каждым действием присваивания. Условие 1 удовлетворяется, если предикат I истинен в начальном состоянии каждого процесса. Условие 2 удовлетворяется, если для любого действия присваивания а предикат I истинен после выполнения а при условии, что I был истинным до выполнения а. Таким образом, эти два условия образуют пример использования математической индукции.
Предположим, что предикат I является глобальным инвариантом. Допустим, что любое критическое утверждение С в обосновании каждого процесса Рэ
имеет вид I L, где L — предикат относительно локальных переменных. В частности, каждая переменная, на которую ссылается предикат L, является либо локальной переменной для процесса Р:, либо глобальной, которой присваивает только процесс Р:. Если все критические утверждения можно представить в форме I L, то доказательства правильности процессов будут свободны от взаимного вмешательства. Дело в том, что: 1) предикат I инвариантен относительно каждого действия присваивания а, и 2) ни одно действие присваивания в одном процессе не может повлиять на локальный предикат L в другом процессе, поскольку левая часть присваивания а отличается от переменных в предикате L.
Если все утверждения используют глобальный инвариант и локальный предикат так, как описано выше, требование взаимного невмешательства (2.5) выполняется для каждой пары действий присваивания и критических утверждений. Кроме того, нам нужно проверить только тройки в каждом процессе, чтобы удостовериться, что каждое критическое утверждение имеет вышеописанный вид, а предикат I является глобальным инвариантом. Нам даже нет необходимости просматривать утверждения или операторы в других процессах. Фактически из массива идентичных процессов достаточно проверить только один. В любом случае нужно проверить лишь линейное число операторов и утверждений. Сравните это с необходимостью проверки экспоненциального количества историй программы (см. раздел 2.1).
70 Часть 1 Программирование с разделяемыми переменными
Техника глобальных инвариантов широко используется в остальной части книги. Ее полезность и мощность мы продемонстрируем в конце данного раздела после знакомства с четвертым способом избежать взаимного вмешательства — синхронизацией.
2.7.4. Синхронизация
Последовательность операторов внутри оператора await для других процессов выступает как неделимая единица. Это значит, что, определяя, вмешиваются ли процессы друг в друга, можно не обращать внимание на результаты выполнения отдельных операторов. Достаточно выяснить, может ли вся последовательность вызывать вмешательство. Например, рассмотрим следующее неделимое действие:
{х = х+1; у = у+1;>
Ни одно присваивание само по себе не может вызвать вмешательства, поскольку никакой другой процесс не может увидеть состояния, в котором переменная х уже была увеличена на единицу, а у — еще нет. Причиной вмешательства может стать только пара присваиваний.
Внутренние состояния сегментов программы внутри угловых скобок также неделимы. Следовательно, ни одно утверждение о внутреннем состоянии программы не может подвергаться вмешательству со стороны другого процесса.
Например, утверждение в середине сле дующего неделимого действия не является критическим.
{х == О л у == 0}
(х = х+1; {х == 1 л у == 0} у = у+1;> I
{х == 1 л у == 1}
Эти два свойства неделимых действий приводят к двум способам использования синхронизации для устранения взаимного влияния: взаимному исключению и условной синхронизации. Рассмотрим следующий фрагмент.
со Р1: ... а; ...
// Р2: ... S1; {С} S2; ...
ос
Здесь а — это оператор присваивания в процессе PI, a S1 и S2 — операторы в процессе Р2. Критическое утверждение С является предусловием оператора S2.
Предположим, что а влияет на С. Один способ избавиться от этого — использовать взаимное исключение, чтобы "скрыть" утверждение С от оператора а. Для этого операторы S1 и S2 второго процесса можно собрать в единое неделимое действие.
(SI; S2;>
Теперь операторы S1 и S2 выполняются неделимым образом, и состояние с становится невидимым для других процессов.
Другой способ избежать взаимного влияния процессов — использовать условную синхронизацию, чтобы усилить предусловие оператора а. В частности, можно заменить а следующим условным неделимым действием.
(await ('С or В) а;)
Здесь в — предикат, характеризующий множество состояний, при которых выполнение а сделает с истинным. Таким образом, в данном выражении вмешательство устраняется либо ожиданием того, что С станет ложным (тогда оператор S2 не сможет выполняться), либо обеспечением того, что выполнение а сделает с истинным (что будет приемлемым для выполнения S2).
2.7.5. Пример: еще раз о задаче копирования массива
В большинстве параллельных программ используется сочетание представленных выше методов. Здесь все они иллюстрируются в одной простой программе: задаче копирования массива
Глава 2. Процессы и синхронизация 71
(см. листинг 2.2). Напомним, что эта программа использует разделяемый буфер buf для копирования содержимого массива а (в процессе производителя) в массив Ь (в процессе потребителя).
Процессы Producer и Consumer в листинге 2. 2 по очереди получают доступ к переменной buf. Сначала Producer помещает первый элемент массива а в переменную buf, затем Consumer извлекает ее, a Producer помещает в переменную buf следующий элемент массива а и так далее. В переменных р и с ведется подсчет числа помещенных и извлеченных элементов, соответственно. Для синхронизации доступа к переменной buf используются операторы await. Когда выполняется условие р == с, буфер пуст (последний помещенный в него элемент был извлечен). Когда выполняется условие р > с, буфер заполнен.
Допустим, что вначале элементы массива а[п] содержат некоторый набор значений А [п]. (А [ i ] — это просто заменители произвольных действительных значений.) Цель — доказать, что при условии завершения программы, представленной выше, значения элементов b[n] будут совпадать с А[n], т.е. значениями элементов массива а. Это утверждение можно доказать с помощью следующего глобального инварианта.
PC: с <= р <= с+1 л а[0:n-1] == А[0:п-1] Л (р == с+1) => (buf == А[р-1])
Процессы чередуют доступ к переменной buf, поэтому в любой момент значение р равно с или на 1 больше, чем с. Массив а не изменяется, так что значением a[i] всегда является A[i]. Наконец, когда буфер полон (т.е. р == с+1), он содержит А [р-1].
Предикат PC в начальном состоянии является истинным, поскольку переменные рис равны нулю. Его истинность сохраняется каждым оператором присваивания, что показано в схеме доказательства (листинг 2.3). В листинге IP является инвариантом цикла в процессе Producer, а 1C— в Consumer. Как показано, предикаты 1Ри 1C связаны с предикатом PC.
Листинг 2.3 — это еще один пример схемы доказательства, поскольку перед каждым оператором и после него находятся утверждения, и каждая тройка в схеме доказательства истинна. Тройки в каждом процессе образуются непосредственно вокруг операторов присваивания в каждом процессе. Если каждый процесс непрерывно получает возможность выполняться, то операторы await завершаются, поскольку сначала истинно одно условие задержки, затем другое и так далее.
Таким образом, каждый процесс завершается после n итераций. Когда программа завершается, постусловия обоих процессов истинны. Следовательно, заключительное состояние программы удовлетворяет предикату:
PC ^ р == n ^ IC ^ с == n
Таким образом, массив b содержит копию массива а.
Утверждения в двух указанных процессах не оказывают взаимного влияния. Большинство из них являются комбинациями глобального инварианта PC и локальных предикатов. Следовательно, они соответствуют требованиям взаимного невмешательства, описанным в начале раздела о глобальных инвариантах. Четырьмя исключениями являются утверждения, которые определяют отношения между значениями разделяемых переменных рис. Но они не подвержены влиянию из-за операторов await.
Роль операторов await в программе копирования массива— обеспечить чередование доступа к буферу процесса-потребителя и процесса-производителя. В устранении взаимного вмешательства чередование играет двоякую роль. Во-первых, оно гарантирует, что два процесса не получат доступ к переменной buf одновременно (это пример взаимного исключения). Во-вторых, оно гарантирует, что производитель не перезаписывает элементы (переполнение), а потребитель не читает их дважды ("антипереполнение") — это пример условной синхронизации.
Подводя итоги, отметим, что этот пример, несмотря на простоту, иллюстрирует все четыре способа избежать взаимного влияния. Во-первых, многие операторы и многие части утверждений в каждом процессе не пересекаются. Во-вторых, использованы ослабленные утверждения о разделяемых переменных; например, говорится, что условие buf == А [р-1]
72 Часть 1 Программирование с разделяемыми переменными
истинно, только если истинно р == с+1. В-третьих, для выражения отношения между значениями разделяемых переменных использован глобальный инвариант PC; хотя при выполнении программы изменяется каждая переменная, это отношение не меняется! И, наконец, чтобы обеспечить взаимное исключение и условную синхронизацию, необходимые в этой программе, использована синхронизация, выраженная операторами await.
