Сеточные вычисления

Дифференциальные уравнения в частных производных (partial differential equations — PDE) применяются для моделирования разнообразных физических систем: прогноза погоды, обтекания крыла потоком воздуха, турбулентности в жидкостях и т.д. Некоторые простые PDE можно решить прямыми методами, но обычно нужно найти приближенное решение уравнения на конечном множестве точек, применяя итерационные численные методы. В этом разделе показано, как решить одно конкретное PDE — двухмерное уравнение Лапласа — с помощью сеточных вычислений по так называемому методу конечных разностей. Но при решении других PDE и в других приложениях сеточных вычислений, например, при обработке изображений, используется такая же техника программирования.

Для решения уравнения Лапласа существует несколько итерационных методов: Якоби, Гаусса—Зейделя, последовательная сверхрелаксация (successive over-relaxation — SOR) и многосеточный. Вначале будет показано, как запрограммировать метод итераций Якоби (с помощью разделяемых переменных и передачи сообщений), поскольку он наиболее прост и легко распараллеливается. Затем покажем, как программируются другие методы, сходя­щиеся гораздо быстрее. Их алгоритмы сложнее, но схемы взаимодействия и синхронизации в параллельных программах для них аналогичны.

11.1.2. Метод последовательных итераций Якоби

В методе итераций Якоби новое значение в каждой точке сетки равно среднему из преды­дущих значений четырех ее соседних точек (слева, справа, сверху и снизу). Этот процесс по­вторяется, пока вычисление не завершится. Ниже строится простая последовательная про­грамма и приводится ряд оптимизаций кода, повышающих производительность программы.

Предположим, что сетка представляет собой квадрат размером пхп и окружена квадратом граничных точек. Одна матрица нужна для представления области и ее границы, другая — для хранения новых значений.

real  gridfOin+l,0:n+l],   new[0:n+l,0:n+l];

Границы обеих матриц инициализируются соответствующими граничными условиями, а внутренние точки — некоторым начальным значением, например 0. (В первом из последую­щих алгоритмов граничные значения в матрице new не нужны, но они понадобятся позже.)

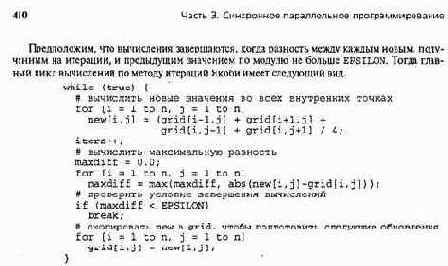
Здесь maxdif f имеет действительный тип, iters — целый (это счетчик числа фаз обновле­ния). В программе предполагается, что массивы хранятся в памяти машины по строкам; если же массивы хранятся по столбцам (как в Фортране), то в циклах for сначала должны быть итерации по j, а затем по 1.

Приведенный выше код корректен, но не очень эффективен. Однако его производитель­ность можно значительно повысить. Для этого рассмотрим каждую часть программы и сдела­ем ее более эффективной.

В первом цикле for присваивания выполняются п2 раз в каждой фазе обновлений. Сум­мирование оставим без изменений, а деление на 4 заменим умножением на 0.25. Такая за­мена повысит производительность, поскольку умножение выполняется быстрее, чем деление. Очевидно, что данная операция выполняется много раз, поэтому улучшение будет заметным. Такая оптимизация называется сокращением мощности, поскольку заменяет "мощное" (дорогое) действие более слабым (дешевым). (В действительности для целых значений деле­ние на 4 можно заменить еще более слабым действием — смещением вправо на 2.)

Рассмотрим часть кода, в которой вычисляется максимальная разность. Эта часть выпол­няется на каждой итерации цикла while, но только один раз приводит к выходу из цикла. Намного эффективней заменить цикл while конечным циклом, в котором итерации выпол­няются определенное количество раз. По существу, iters и maxdif f меняются ролями. Вместо того, чтобы подсчитывать число итераций и использовать maxdif f для завершения вычислений, iters теперь используется для управления количеством итераций. Тогда мак­симальная разность будет вычисляться только один раз после главного цикла вычислений. После проведения этой и первой оптимизаций программа примет следующий вид.







412                                                         Часть 3. Синхронное параллельное программирование

Развертывание цикла само по себе мало влияет на рост производительности, но часто позволяет применить другие оптимизации.21



Например, в последнем коде больше не нужно менять места­ми роли матриц. Достаточно переписать второй цикл обновлений так, чтобы данные считыва­лись из new, полученной в первом цикле обновлений, и записывались в старую матрицу grid. Но тогда трехмерная матрица не нужна, и можно вернуться к двум отдельным матрицам!

В листинге 11.1 представлена оптимизированная программа для метода итераций Якоби. Проведены четыре оптимизации исходного кода: 1) деление заменено умножением; 2) для за­вершения вычислений использовано конечное число итераций, а максимальная разность вы­числяется только один раз; 3) две матрицы скомбинированы в одну с дополнительным изме­рением, что избавляет от копирования матриц; 4) цикл развернут дважды и его тело перепи­сано, поскольку дополнительный индекс и операторы изменения ролей матриц не нужны. В действительности в данной задаче можно было бы перейти от второй оптимизации прямо к четвертой. Однако третья оптимизация часто полезна.



Глава 11. Научные вычисления                                                                                                      413

11.1.3. Метод итераций Якоби с разделяемыми переменными

Рассмотрим, как распараллелить метод итераций Якоби. В листинге 3.16 был приведен пример программы, параллельной по данным. В ней на одну точку сетки приходился один процесс, что дает степень параллельности, максимально возможную для данной задачи. Хотя программа эффективно работала бы на синхронном мультипроцессоре (SIMD-машине), в ней слишком много процессов, чтобы она могла эффективно выполняться на обычном MIMD-мультипроцессоре. Дело в том, что каждый процесс выполняет очень мало работы, поэтому во времени выполнения программы будут преобладать накладные расходы на пере­ключение контекста. Кроме того, каждому процессу нужен свой собственный стек, поэтому, если сетка велика, программа может не поместиться в памяти. Следовательно, производи­тельность параллельной программы окажется гораздо хуже, чем последовательной.



Предположим, что есть PR процессоров, и размерность сетки п намного больше PR. Что­ бы параллельная программа была эффективной, желательно распределить вычисления между процессорами поровну. Для данной задачи сделать это несложно, поскольку для обновления каждой точки сетки нужно одно и то же количество работы. Следовательно, можно использо­вать PR процессов так, чтобы каждый из них отвечал за одно и то же число точек сетки. Мож­но разделить сетку на PR прямоугольных блоков или прямоугольных полос. Используем по­лосы, поскольку для них немного проще написать программу. Вероятно также, что использо­вание полос более эффективно, поскольку при длинных полосах локальность данных выше, чем при коротких блоках, что оптимизирует использование кэша данных.

Предположив для простоты, что n кратно PR, а массивы хранятся в памяти по строкам, назначим каждому процессу горизонтальную полосу размера n/PR x п. Каждый процесс обновляет свою полосу точек. Однако, поскольку процессы имеют общие точки, располо­женные на границах полос, после каждой фазы обновлений нужна барьерная синхронизация для того, чтобы все процессы завершили фазу обновлений перед тем, как любой процесс нач­нет выполнять следующую.

В листинге 11.2 приведена параллельная программа для метода итераций Якоби с разделяе­мыми переменными. Использован стиль "одна программа— много данных" (single program, multiple data — SPMD): каждый процесс выполняет один и тот же код, но обрабатывает различ­ные части данных. Здесь каждый рабочий процесс сначала инициализирует свои полосы, вклю­чая границы, в двух матрицах. Тело каждого рабочего процесса основано на программе в лис­тинге 11.1. Барьерная синхронизация происходит с помощью разделяемой процедуры, реали­зующей один из алгоритмов в разделе 3.4. Для достижения максимальной эффективности можно применить симметричный барьер, например, барьер с распространением.





Листинг 11.2 также иллюстрирует эффективный способ вычисления максимальной разно­сти во всех парах окончательных значений в точках сетки.


Каждый рабочий процесс вычисля­ ет максимальную разность для точек в своей полосе, используя локальную переменную ту-dif f, а затем сохраняет полученное значение в массиве максимальных разностей. После вто­рого барьера каждый рабочий процесс может параллельно вычислить максимальное значение в maxdif f [ * ] (все эти вычисления можно также проводить только в одном рабочем процес­се). Локальные переменные в каждом процессе позволяют избежать использования критиче­ских секций для защиты доступа к единственной глобальной переменной, а также конфлик­тов в кэше, которые могли бы возникнуть из-за ложного разделения массива maxdif f.

Программа в листинге 11.2 могла бы работать немного эффективнее, если встроить вызовы процедуры barrier. Однако встраивание кода вручную сделает программу тяжелой для чтения. Поэтому лучше всего использовать компилятор, поддерживающий оптимизацию встраивания.

11.1.4. Метод итераций Якоби с передачей сообщений

Рассмотрим реализацию метода итераций Якоби на машине с распределенной памятью. Можно было бы использовать реализацию распределенной разделяемой памяти (раздел 10.4) и просто взять программу из листинга 11.2. Однако такая реализация не всегда доступна и вряд ли дает наилучшую производительность. Как правило, эффективнее написать про­грамму с передачей сообщений.

Один из способов написать параллельную программу с передачей сообщений — модифици­ровать программу с разделяемыми переменными. Сначала разделяемые переменные распреде­ляются между процессами, затем в тех местах, где процессам нужно обменяться данными, до­бавляются операторы отправки и получения. Другой способ— сначала изучить парадигмы взаимодействия процессов, описанные в разделах 9.1—9.3 (портфель задач, алгоритм пульсации и конвейер), и выбрать подходящую. Часто, как в нашем примере, можно использовать оба метода.

Начав с программы в листинге 11.2, вновь используем PR рабочих процессов, обновляю­щих каждый раз полосу точек сетки. Распределим массивы grid и new так, чтобы полосы были локальными для соответствующих рабочих процессов.


Также нужно продублировать строки на краях полос, поскольку рабочие не могут считывать данные, размещенные в других процессах. Таким образом, каждому процессу нужно хранить точки не только своей полосы, но и границ соседних полос. Каждый процесс выполняет последовательность фаз обновле­ния; после каждого обновления он обменивается краями своей полосы с соседями. Такая схема обмена соответствует алгоритму пульсации (см. раздел 9.2). Обмены заменяют точки барьерной синхронизации в листинге 11.2.                                                                                i

Глава 11. Научные вычисления                                                                                                415

Нужно также распределить вычисление максимальной разности после того, как каждый процесс завершит обновление в своей полосе сетки. Как и в листинге J 1.2, каждый процесс просто вычисляет максимальную разность в своей полосе. Затем выбирается один процесс, который собирает все полученные значения. Все это можно запрограммировать, используя либо сообщения, передаваемые от процесса к процессу, либо коллективное взаимодейст­вие, как в MPI (раздел 7.8).

В листинге 11.3 представлена программа для метода итераций Якоби с передачей сообще­ний. В каждой из двух фаз обновления используется алгоритм пульсации, поэтому соседние процессы дважды обмениваются краями во время одной итерации главного вычислительного цикла. Первый обмен программируется следующим образом.

if   (w >  1)     send up[w-l](new[l,*]);

if   (w <  PR)   send down[w+1](new[HEIGHT,*]);

if   (w <  PR)   receive up[w](new[HEIGHT+l,*]);

if   (w > 1)     receive down[w](new[0,*]);

Все процессы, кроме первого, отправляют верхний ряд своей полосы соседу сверху. Все про­цессы, кроме последнего, отправляют нижний ряд своей полосы соседу снизу. Затем каждый получает от своих соседей края; они становятся границами его полосы. Второй обмен иден­тичен первому, только вместо new используется grid.





416                                                      Часть 3. Синхронное параллельное программирование

После подходящего числа итераций каждый рабочий процесс вычисляет максимальную разность в своей полосе, затем первый из них собирает полученные значения. Как отмече­но в конце листинга, глобальная максимальная разность равна окончательному значению mydif f в первом процессе.

Программу в листинге 11.3 можно оптимизировать. Во-первых, для данной программы и многих других сеточных вычислений нужно проводить обмен краями после каждой фазы об­новлений. Здесь, например, можно обменивать края после каждой второй фазы обновлений. Это вызовет "скачки" значений в точках на краях, но, поскольку алгоритм сходится, он все рав­но будет давать правильный результат. Во-вторых, можно перепрограммировать оставшийся обмен так, чтобы между отправкой и получением сообщений выполнялись локальные вычисле­ния. Например, можно реализовать взаимодействие, при котором каждый рабочий: 1) отправляет свои края соседям; 2) обновляет внутренние точки своей полосы; 3) получает края от соседей; 4) обновляет края своей полосы. Такой подход значительно повысит вероятность того, что края от соседей придут раньше, чем они нужны, и, следовательно, задержки операций получения не будет. В листинге 11.4 представлена оптимизированная программа. Предлагаем читателю срав­нить производительность и результаты последних двух программ с передачей сообщений.



Глава 11. Научные вычисления                                                                                                417

11.1.5. Последовательная сверхрелаксация по методу "красное-черное"

Метод итераций Якоби сходится очень медленно, поскольку для того, чтобы значения неко­торой точки повлияли на значения удаленных от нее точек, нужно длительное время. Например, нужны п/2 фаз обновлений, чтобы влияние граничных значений сетки дошло до ее центра.

Схема Гаусса—Зейделя (GS) сходится намного быстрее и к тому же использует меньше памяти.


Новые значения в точках вычисляются с помощью комбинации старых и новых зна­ чений соседних точек. Проход по сетке слева направо и сверху вниз образует развертку, почти как для телевизионных изображений на электронно-лучевой трубке. Новые точки вычисля­ются на месте следующим образом.



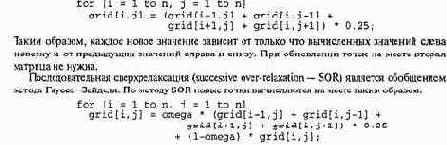
Переменная omega называется параметром релаксации; ее значение выбирается из диапазо­на 0 < omega < 2. Если omega равна 1, то метод SOR сводится к методу Гаусса—Зейделя. Ес­ли ее значение равно 0.5, новое значение точки сетки есть половина среднего значения ее соседей плюс половина ее старого значения. Выбор подходящего значения omega зависит от решаемого дифференциального уравнения в частных производных и граничных условий.

Хотя методы GS и SOR сходятся быстрее, чем метод итераций Якоби„ и требуют вдвое меньше памяти, непосредственно распараллелить их непросто, поскольку при обновлении точ­ки используются как старые, так и новые значения. Другими словами, методы GS и SOR позво­ляют обновлять точки на месте именно потому, что применяется последовательный порядок об­новлений. (В циклах этих двух алгоритмов присутствует так называемая зависимость по данным. Их можно распараллелить, используя волновые фронты. Оба вопроса обсуждаются в разделе 12.2.)

К счастью, GS и SOR можно распараллелить, слегка изменив сами алгоритмы (их сходи­мость сохранится). Сначала покрасим точки в красный и черный цвет, как клетки шахматной доски. Начав с верхней левой точки, окрасим точки через одну красным цветом, а остальные — черным. Таким образом, у красных точек будут только черные соседи, а у чер­ных — только красные. Заменим единый цикл в фазе обновлений двумя вложенными: в пер­вом обновляются значения красных точек, а во втором — черных.

Теперь схему "красное-черное" можно распараллелить: у красных точек все соседи только черного цвета, а у черных — красного. Следовательно, все красные точки можно обновлять параллельно, поскольку их значения зависят только от старых значений черных точек.


Так же обновляются и черные точки. Однако после каждой фазы обновлений нужна барьерная синхронизация, чтобы перед началом обновления черных точек было завершено обновление всех красных точек и наоборот.

В листинге 11.5 приведена параллельная программа для метода "красное-черное" по схе­ме Гаусса—Зейделя, использующая разделяемые переменные. (Последовательная сверхрелак­сация отличается только выражением для обновления точек.) Вновь предположим, что есть PR рабочих процессов и п кратно PR. Разделим сетку на горизонтальные полосы и назначим каждому процессу по одной полосе.



По структуре программа идентична представленной в листинге 11.2 программе для метода итераций Якоби. Более того, максимальная разность вычисляется здесь точно так же. Однако теперь в каждой фазе вычислений обновляется вдвое меньше точек по сравнению с соответ­ствующей фазой в параллельной программе для метода итераций Якоби. Соответственно, и внешний цикл выполняется вдвое большее число раз. Это приводит к удвоению числа барь­еров, поэтому дополнительные расходы из-за барьерной синхронизации будут составлять бо­лее значительную часть от общего времени выполнения. С другой стороны, при одном и том же значении MAXITERS данный алгоритм приведет к лучшим результатам (или к сравнимым результатам при меньших значениях maxiters).

Метод "красное-черное" можно запрограммировать, используя передачу сообщений. Программа будет иметь такую же структуру, как и соответствующая программа для метода

Глава 11. Научные вычисления                                                                                                      419

итераций Якоби (листинги 11.3 или 11.4). Как и раньше, каждый рабочий процесс отвечает за обновление точек своей полосы, и соседним процессам нужно обмениваться краями после каждой фазы обновлений. Красные и черные точки на краях можно обменивать отдельно, но, если они обмениваются вместе, нужно меньше сообщений.

Мы предположили, что отдельные точки окрашены в красный или черный цвет.


В резуль­тате i и j пошагово увеличиваются на два во всех циклах обновлений. Это приводит к слабо­му использованию кэша: в каждой фазе обновлений доступна вся полоса целиком, но из двух соседних точек читается или записывается только одна.22 Можно повысить производитель­ность, окрашивая блоки точек, как квадраты на шахматной доске, состоящие из множеств то­чек. Еще лучше окрасить полосы точек. Например, разделить каждую полосу рабочего попо­лам (по горизонтали) и закрасить верхнюю половину красным цветом, а нижнюю — черным. В листинге 11.5 каждый рабочий многократно обновляет сначала красные, затем черные точ­ки, и после каждой фазы обновлений установлен барьер. В каждой фазе обновлений доступна только половина всех точек (каждая и читается, и записывается).

11.1.6. Многосеточные методы

Если при аппроксимации уравнений в частных производных используются сеточные вычисления, зернистость сетки влияет на время вычислений и точность решения. На гру­бых (крупнозернистых) сетках решение находится быстрее, но упускаются некоторые его подробности. Мелкие сетки дают более точные решения, но за большее время. Моделиро­вание физических систем обычно включает развитие системы во времени, поэтому сеточ­ные вычисления нужны на каждом временном шаге. Это обостряет противоречия между временем вычислений и точностью решения.

Предсказание погоды является типичным приложением такого рода. Процесс моделиро­вания погоды начинается с текущих условий (температура, давление, скорость ветра и т.п.), а затем для предсказания будущих условий проходит по временным шагам. Предположим, нужно сделать прогноз для континентальных США (без Аляски), используя сетку с разреше­нием в одну милю. Тогда понадобятся около 3000 х 1500 (4,5 миллиона) точек и вычисления такого масштаба на каждом временном шаге! Чтобы учесть значительное влияние океанов, нужна еще большая сетка. Однако с сеткой такого размера прогноз может безнадежно опо­здать! Используя более грубую сетку с разрешением, скажем, 10 миль, вычисления можно бу­дет завершить достаточно быстро, но, возможно, "потеряв" локальные возмущения.



Для достаточно быстрого и результативного решения подобных задач существует два под­хода. Один из них состоит в применении адаптивной сетки. При этом подходе зернистость сетки непостоянна. Она грубая там, где решение относительно однородно, и точная, где ре­шение нуждается в детализации. Кроме того, зернистость может не быть постоянной, чтобы адаптироваться к изменениям, происходящим по мере имитации. Например, на плоской рав­нине и под центрами высокого давления погода, как правило, однородна, но варьируется вблизи гор и быстро изменяется на границах фронтов.

Второй способ быстрого решения задач большого размера состоит в применении множе­ственных сеток. Используются сетки различной зернистости и переходы между ними в ходе вычислений, чтобы ускорить сходимость на самой точной сетке. Многосеточные методы ис­пользуют так называемую коррекцию грубой сетки, состоящую из следующих этапов.

•    Начать с точной сетки и обновить точки путем нескольких итераций, применив один из методов релаксации (Якоби, Гаусса—Зейделя, последовательной сверхрелаксации).

•    Ограничить полученный результат более грубой сеткой, точки которой вдвое дальше друг от друга. Соответствующие граничные точки имеют одни и те же значения на

22

Сгенерированный машинный код будет выполняться медленнее еще и потому, что в нем больше ко­манд ветвления. Кроме того, увеличение параметра цикла на два может выполняться медленнее, чем на один



Глава 11. Научные вычисления                                                                                                     421

Значение в точке грубой сетки копируется в соответствующую точку точной сетки, половина его копируется в четыре ближайшие точки точной сетки, а четверть — в четыре точки, бли­жайшие по диагонали. Таким образом, точка точной сетки, расположенная между двумя точ­ками грубой сетки, получает по половине их значений, а точка в центре квадрата из четырех точек грубой сетки получает по четверти их значений.



С помощью описанного оператора интерполяции можно инициализировать внутренние точки точной сетки следующим образом. Сначала присвоить точки грубой сетки соответст­вующим точкам точной.

fine[i,j]   = coarse[x,у];

Затем обновить другие точки точной сетки в столбцах, которые только что были обновлены. Одно такое присвоение имеет следующий вид.

fine[i-l,j]   =   (fine[1-2,3]   +  fine[i,j])   *   0.5;

Наконец обновить остальные точки точной сетки (в столбцах, состоящих только из точек на рис. 11.2), присвоив каждой из них среднее арифметическое значений в соседних точках ее строки. Одно присвоение имеет такой вид.

fine[i-l,3-U   =   (fine[i-l,j-2]   +  fine[i-l,j])   *  0.5;

Таким образом, значение в точке, расположенной в той же строке, что и точки грубой сетки, равно среднему арифметическому значений в ближайших точках грубой сетки, а в точке, рас­положенной в другой строке, — среднему значений, соседствующих по горизонтали, т.е. чет­верти суммы значений в четырех ближайших точках грубой сетки.

Существует несколько видов многосеточных методов. В каждом из них используются раз­ные схемы коррекции грубой сетки. В простейшем методе используется одна коррекция: вна­чале на точной сетке выполняем несколько итераций, переходим на грубою сетку и решаем задачу на ней, затем интерполируем полученное решение на точную сетку и выполняем на ней еще несколько итераций. Такая схема называется двухуровневым V-циклом.

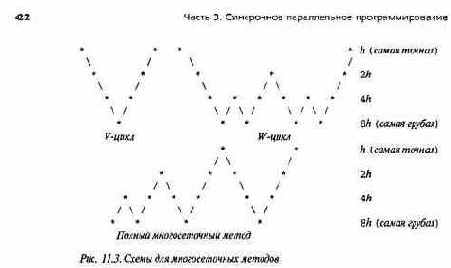
На рис. 11.3 показаны три общие многосеточные схемы, в которых используются четыре различных размера сеток. Если расстояние между точками самой точной сетки равно А, то расстояние между точками других сеток — 2h, 4h и 8h (рис. 11.3). V-цикл в общем виде имеет несколько уровней: вначале на самой точной сетке выполняем несколько итераций, перехо­дим к более грубой сетке, снова выполняем несколько итераций, и так до тех пор, пока не окажемся на самой грубой сетке. На ней решим задачу. Затем интерполируем полученное решение на более точною сетку, выполним несколько итераций, и так далее, пока не прове­дем несколько итераций на самой точной сетке.



W-цикл повышает точность с помощью многократных переходов между сетками. На более грубых сетках проводятся дополнительные релаксации, и снова, как обычно, точное решение задачи находится на самой грубой сетке.

В полном многосеточном методе различные сетки используются столько же раз, сколько ив W-цикле, но при этом достигаются более точные результаты. В нем перед тем, как впер­вые использовать самую точную сетку, несколько раз выполняются вычисления на более гру­бых сетках, поэтому начальные значения для самой точной сетки оказываются правильнее. Полный многосеточный метод основан на рекуррентной последовательности шагов: 1) создаем начальное приближение к решению на самой грубой сетке, затем вычисляем на ней точное решение; 2) переходим к более точной сетке, выполняем на ней несколько итера­ций, возвращаемся к более грубой сетке и вновь находим на ней точное решение; 3) повторяем этот процесс, каждый раз поднимаясь на один уровень выше, пока не окажемся на самой точной сетке, после чего проходим полный V-цикл.

Многосеточные методы сходятся намного быстрее, чем основные итерационные. Однако программировать их намного сложнее, поскольку в них обрабатываются сетки различных размеров и нужны постоянные переходы между ними (ограничения и интерполяции)



Имея последовательную программу для многосеточного метода, можно разделить каждую решетку на полосы и распараллелить процессы ограничения, обновления и интерполяции практически так же, как были распараллелены методы итераций Якоби и Гаусса—Зейделя. В программе с разделяемыми переменными после каждой фазы нужны барьеры, а в программе с передачей сообщений — обмен краями полос. Однако получить хорошее ускорение с по­мощью параллельной многосеточной программы непросто. Переходы между сетками и до­полнительные точки синхронизации увеличивают накладные расходы. Кроме того, многосе­точный метод дает хороший результат быстрее, чем простая итерационная схема, за счет того, что на всех сетках, кроме самой грубой, выполняется лишь несколько итераций.В результате накладные расходы занимают большую часть общего времени выполнения. И все же разум­ное ускорение достижимо, особенно на сетках очень больших размеров, а именно к ним и применяются многосеточные методы.


Содержание раздела

---

---