Распараллеливающие компиляторы
Главной темой этой книги является создание явно параллельных программ, т.е. программ, в которых программист должен определить процессы, разделить между ними данные и запрограммировать все необходимые взаимодействия и синхронизацию. Явно параллельная программа — вот что в конечном счете может выполняться на многопроцессорных машинах. Однако существуют и другие подходы к разработке параллельных программ. В данном разделе рассматриваются распараллеливающие компиляторы, которые преобразуют последовательные программы в параллельные. В следующем разделе описываются высокоуровневые подходы на основе языков с поддержкой параллельных данных и функциональных языков.
При распараллеливании программы необходимо определить задачи, которые не зависят друг от друга и, следовательно, могут выполняться одновременно. Некоторые программы являются существенно параллельными, т.е. содержащими огромное число независимых задач, например, умножение матриц или вычисление множеств Мандельброта. Однако большинство программ состоят из частей, которые зависят друг от друга и требуют периодической синхронизации при выполнении. Например, взаимодействующим процессам необходимо синхронизироваться в программе типа "производитель-потребитель". Или процессам в сеточных вычислениях нужна барьерная синхронизация после каждой фазы обновлений.
Цель распараллеливающего компилятора — получить последовательную программу и создать корректную параллельную Для этого он выполняет так называемый анализ зависимости. Компилятор определяет, какие части последовательной программы независимы (и являются кандидатами на параллельное выполнение), а какие зависят друг от друга и требуют последовательного выполнения или какой-то другой формы синхронизации. Поскольку большинство вычислений в последовательной программе происходит внутри циклов, особенно вложенных, основным для компилятора является распараллеливание циклов.
В этом разделе определяются различные виды зависимости по данным и демонстрируется, как компилятор выполняет анализ зависимости.
Затем рассматриваются некоторые наи более распространенные преобразования последовательных циклов в параллельные. Подробнее они описаны в литературе, указанной в исторической справке в конце главы.
Распараллеливающие компиляторы постоянно совершенствуются и в настоящее время вполне пригодны для создания эффективных параллельных программ с разделяемыми переменными. Особенно это касается научных программ, содержащих много циклов и длительных вычислений. Однако создать хорошую программу с обменом сообщениями гораздо сложнее, поскольку всегда существует много вариантов структуры программы и взаимодействия, как было показано в главе 11. Кроме того, некоторые сложные последовательные алгоритмы трудно распараллелить, например, многосеточные методы или метод Барнса—Хата.
12.2.1. Анализ зависимости
Предположим, что последовательная программа содержит два оператора S, и S2, причем S, находится перед S2. Говорят, что между двумя операторами существует зависимость по
Глава 12. Языки, компиляторы, библиотеки и инструментальные средства 459
данным, если они считывают или записывают данные в общей области памяти так, что порядок их выполнения нельзя изменять. Существует три основных типа зависимости по данным."
1. Потоковая зависимость. Оператор S2
потоково зависит от S,, если S2 считывает из ячейки, в которую записывает S,. (Такая зависимость еще называется истинной.)
2. Антизависимость. Оператор S2 является антизависимым относительно St, если S2
записывает в ячейку, из которой 5, считывает.
3. Зависимость по выходу. Оператор S2 зависит по выходу от Slt
если оператор S2
записывает данные в ту же ячейку памяти, что и S,.
Будем просто говорить, что S3 зависит от St, если это зависимость по данным; тип зависимости не важен.
В качестве примера рассмотрим следующую последовательность операторов.
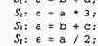
Оператор S2 потоково зависит от St, поскольку считывает а. Оператор S, антизависим относительно S2, поскольку он записывает а; .5", также зависит по выходу от S,, поскольку они оба записывают а.
Наконец, оператор S, потоково зависит от S3, поскольку считывает а. (St также потоково зависит от St, но St
должен выполняться перед S}.) Вследствие этих зависимостей операторы должны выполняться в порядке, указанном в списке; изменение порядка операторов приведет к изменению результатов.
Зависимости по данным легко определить в последовательном коде, содержащем ссылки только на скалярные переменные. Намного сложнее определить зависимости в циклах и при ссылках в массивы (которые обычно встречаются вместе), поскольку ссылки в массивы имеют индексы, а в индексах обычно используются параметры циклов, т.е. индексы массива имеют различные значения на разных итерациях цикла. В действительности общая проблема вычисления всех зависимостей по данным в программе неразрешима из-за применения синонимов имени массива, которое может возникнуть при использовании указателей или вызовов функций внутри индексных выражений. Даже если указатели не разрешены, как в Фортране, и индексные выражения являются линейными функциями, проблема является NP-трудной, т.е. эффективного алгоритма для нее, по всей вероятности, нет.
Чтобы лучше понять проблемы, создаваемые циклами и массивами, рассмотрим еще раз код прямого хода в решении системы уравнений (см. листинг 11.12).

В каждой итерации внешнего цикла S2 зависит от -У,, a S3 зависит и от «У,, и от S2. Внутренний цикл состоит из одного оператора, поэтому никакой зависимости в этом цикле нет. Однако внутренний цикл приводит к зависимости S2 от самого себя, поскольку S2
и считывает, и записывает sum. Аналогично и внешний цикл создает зависимость: S2 зависит от S}, поскольку значение, записанное в х [ i ] на одной итерации внешнего цикла, считывается на всех последующих.
Четвертый тип зависимости — по входу; она обычно возникает, когда два оператора считывают данные из одной и той же ячейки памяти. Зависимость по входу не ограничивает порядок выполнения операторов.
460 Часть 3 Синхронное параллельное программирование
Проверка зависимости представляет собой задачу определения, есть ли зависимость по данным в произвольной паре индексированных ссылок. В общем виде задача ставится для вложенного цикла следующего вида.
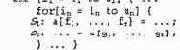
Есть п вложенных циклов и, соответственно, п индексных переменных. Нижние и верхние границы п индексных переменных определяются функциями 1J
и и;. Наиболее глубоко вложенный цикл состоит из двух операторов, содержащих ссылки на элементы n-мерного массива а; первый оператор записывает в а, второй — считывает из а. Вызовы функций f, и д: в этих операторах содержат в качестве своих аргументов индексные переменные; функции возвращают значения индексов.
Итак, возникает следующий вопрос о зависимости в данном цикле: существуют ли значения индексных переменных, при которых f, = g,, f 2 = g2 и т.д.? Ответ определяет, зависит 52
от 5, на одной и той же итерации цикла или между операторами есть зависимости, создаваемые циклом.
Проверку зависимости можно представить в виде специальной системы линейных уравнений и неравенств следующего вида.
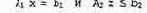
Коэффициенты в матрицах А, и А, определяются функциями f и g в программе, а значения в векторах Ь, и Ь2 — границами для индексных переменных. Решением первого уравнения является присваивание значений индексным переменным, при котором ссылки массива перекрываются. Второе уравнение (в действительности система неравенств) обеспечивает, что значения индексных переменных находятся внутри границ, определяемых функциями 1 и и. Решение данной задачи похоже на решение двух систем линейных уравнений, рассмотренное в разделе 11.3, однако имеет два принципиальных отличия: 1) решение должно быть вектором целых, а не действительных чисел, 2) второе выражение имеет соотношение "меньше или равно". Именно эти отличия приводят к тому, что проблема становится NP-трудной, даже если индексные выражения являются линейными функциями и не содержат указателей. (Проверка зависимости при этих условиях эквивалентна частному случаю задачи целочисленного линейного программирования.)
Хотя проверка зависимости является сложной (а в худшем случае — неразрешимой) задачей, существуют эффективные проверки, применимые в некоторых частных случаях. В действительности почти для всех циклов, встречающихся на практике, можно определить, перекрываются ли две ссылки в массив. Например, эффективные проверки существуют для ситуации, при которой все границы циклов являются константами, или границы внутренних циклов зависят только от границ внешних циклов. Цикл прямого хода в методе исключений Гаусса, приведенный выше, удовлетворяет данным ограничениям: границы для i — константы, одна граница для j — константа, а другая зависит от значения i. Но если компилятор не может определить, отличаются ли две ссылки на элементы массива, то он пессимистически предполагает, что зависимость есть.
12.2.2. Преобразования программ
Проверка зависимости является первым этапом в работе распараллеливающего компилятора. Второй шаг — распараллеливание циклов с использованием результатов первого этапа. Ниже на нескольких примерах показано, как это происходит.
В первом примере предположим, что функция f не имеет побочного эффекта, и рассмотрим следующий вложенный цикл.

i еперь можно распараллелить внешний цикл, используя оператор со.
Перестановка циклов — это один из видов преобразования программ, используемых в распараллеливании. Ниже рассматриваются еще несколько полезных преобразований: локализация, расширение скаляра, распределение цикла, слияние циклов, развертка и сжатие, развертка цикла, разделение на полосы, разделение на блоки, а также перекос цикла (рис. 12.1). Они помогают выявлять параллельность, устранять зависимости и оптимизировать использование памяти. Рассмотрим их.
Перестановка циклов Внешний и внутренний циклы меняются местами
Локализация Каждому процессу дается копия переменной
Расширение скаляра Скаляр заменяется элементом массива
Распределение цикла Один цикл расщепляется на два отдельных цикла
Слияние циклов Два цикла объединяются в один
Развертка и сжатие Комбинируются перестановка циклов, разделение на полосы и развертка
Развертка цикла Тело цикла повторяется и выполняется меньше итераций
Разделение на полосы Итерации одного цикла разделяются на два вложенных цикла Разделение на блоки Область итераций разбивается на прямоугольные блоки
Перекос цикла Границы цикла изменяются, чтобы выделить параллельность
фронта волны
Рис. 12.1. Преобразования программ, используемые параллельными компиляторами
Рассмотрим стандартную последовательную программу вычисления матричного произведения с двух квадратных матриц а и b размером пхп.
for [i = 1 to n] for [j = 1 to n] {
27 Для задания параллельных циклов в этой книге используется оператор со. В других языках используются подобные операторы, например parallel do или for all.

i ри оператора в теле второго цикла (по з; зависят друг от друга, поэтому должны выполняться последовательно. Два внешних цикла независимы в действиях с матрицами, поскольку а и b только считываются, а каждый элемент с встречается только один раз. Однако все три цикла создают зависимости, поскольку sum — одна скалярная переменная. Можно распараллелить оба внешних цикла или любой из них, если локализовать sum, т.е. дать каждому процессу собственную копию этой переменной. Таким образом, локализация является преобразованием, устраняющим зависимости.
Другой способ распараллелить программу умножения матриц — применить расширение скаляра. Одиночная переменная заменяется элементом массива. В данном случае можно изменить переменную sum на с [ i, j ]. Это преобразование также позволяет избавиться от последнего оператора присваивания и получить следующую программу.

Два внешних цикла больше не создают зависимости, поэтому теперь можно распараллелить цикл по 1, выполнить перестановку циклов и распараллелить цикл по j или распараллелить оба цикла.2* Наиболее глубоко вложенный цикл в данной программе зависит от инициализации массива с [ i, э ].
Однако элементы массива с можно инициализировать в любом порядке — лишь бы все они инициализировались до начала их использования в вычислениях. Чтобы отделить инициализацию от вычисления произведений во внутреннем цикле, можно применить еще одно преобразование цикла — распределение. При распределении цикла независимые операторы, записанные в теле одного цикла (или вложенных циклов), помещаются в отдельные циклы с одинаковыми заголовками, как в следующем примере.

Теперь для распараллеливания каждого внешнего цикла (по i) можно использовать со. При альтернативном подходе внешние циклы можно объединить и использовать директиву со только один раз, установив между внутренними циклами точку барьерной синхронизации следующим образом.
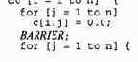
28 В данном примере локализация была бы эффективнее, чем замена скаляра. Во-первых, sum могла бы сохраняться в регистре Во-вторых, ссылки на с [ i, э 1 в полученном коде могут привести к ложному разделению переменных и, как следствие, к слишком непроизводительному использованию кэша.


Глава 12. Языки, компиляторы, библиотеки и инструментальные средства 465
Каждое новое значение а зависит от двух значений, вычисленных в предыдущих итерациях, и от двух значений, которые не обновляются до следующих итераций. На рис. 12.2, а показаны эти зависимости; пунктирными линиями обозначены волновые фронты.

466 Часть 3. Синхронное параллельное программирование