Обзор аксиоматической семантики
В конце раздела 2.1 было описано, как утвердительные рассуждения позволяют понять свойства параллельной программы. Но, что еще важнее, они могут помочь в разработке правильных программ. Поэтому утвердительные рассуждения будут интенсивно использоваться в оставшейся части книги. В этом и следующих двух разделах представлена формальная база для них. В дальнейших главах эти понятия будут использоваться неформально.
Основой для утвердительных рассуждений является так называемая логика программирования — формальная логическая система, которая обеспечивает порождение точных утверждений о выполнении программы. В этом разделе представлены основные понятия данной темы. В исторической справке указаны источники более подробной информации, включающей много различных примеров.
2.6.1. Формальные логические системы
Любая формальная логическая система состоит из правил, определенных в терминах следующих множеств:
• символов',
• формул, построенных из этих символов;
• выделенных формул, называемых аксиомами;
• правил вывода.
Формулами являются правильно построенные последовательности символов. Аксиомы — это особые формулы, которые априори предполагаются истинными. Правила вывода определяют, как получить истинные формулы из аксиом и других истинных формул. Правила вывода имеют вид
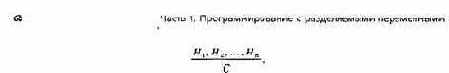
Каждая Я является гипотезой, С — заключением. Значение правила вывода состоит в том, что если все гипотезы истинны, то и заключение истинно. И гипотезы, и заключение являются формулами или их схематическим представлением.
Доказательство в формальной логической системе — это последовательность строк, каждая из которых является аксиомой или может быть получена из предыдущих строк путем применения к ним правила вывода. Теорема — это любая строка в доказательстве. Таким образом, теоремы либо являются аксиомами, либо получены с помощью применения правил вывода к другим теоремам.
Сама по себе формальная логическая система является математической абстракцией — набором символов и отношений между ними.
Логическая система становится интересной, когда формулы представляют утверждения о некоторой обсуждаемой области, а формулы, являющиеся теоремами, — истинные утверждения. Для этого нужно обеспечить интерпретацию формулы.
Интерпретация логики отображает каждую формулу в ложь или истину. Логика является непротиворечивой относительно интерпретации, если непротиворечивы все ее аксиомы и правила вывода. Аксиома непротиворечива, если она отображается в истину. Правило вывода непротиворечиво, если его следствие отображается в истину, при условии, что все его гипотезы отображаются в истину. Следовательно, если логика непротиворечива, то все теоремы являются истинными утверждениями в данной рассматриваемой области. В таком случае ин-'* терпретация называется моделью логики.
Понятие полноты дуально понятию непротиворечивости. Логика является полной относительно интерпретации, если формула, отображаемая в истину, является теоремой, т.е. в данной логике доказуема любая (истинная) формула. Таким образом, если ФАКТЫ— это множество истинных утверждений, выразимых формулами логики, а ТЕОРЕМЫ— множество теорем логики, то непротиворечивость означает, что ТЕОРЕМЫ ФАКТЫ, а полнота— ФАКТЫ с, ТЕОРЕМЫ. Полная и непротиворечивая логика позволяет доказать все ее истинные утверждения.
Как доказал немецкий математик Курт Гедель в своей знаменитой теореме о неполноте, любая логика, которая включает арифметику, не может быть полной. Однако логика, которая расширяет другую логику, может быть относительно полной. Это значит, что она не добавляет неполноту к той, которая присуща расширяемой логике. К счастью, относительной полноты вполне достаточно для логики программирования, представленной здесь, поскольку используемые свойства арифметики безусловно истинны.
2.6.2. Логика программирования
Логика программирования (ЛП) является формальной логической системой, которая позволяет устанавливать и обосновываты(доказывать) свойства программ.
Как и в любой формальной логической системе, в ЛП есть символы, формулы, аксиомы и правила вывода.
Символы ЛП— это предикаты, фигурные скобки и операторы языка программирования. Формулы в Ж? называются тройками. Они имеют вид7 (Р> S {Q}.
Предикаты р и Q определяют отношения между значениями переменных программы; S — это оператор или список операторов.
7 Предикаты в тройках заключаются в фигурные скобки, поскольку это традиционный способ их записи в логиках программирования Однако такие скобки используются в нашей программной нотации и для выделения последовательностей операторов. Во избежание возможных недоразумений предикаты в программе будут записываться с помощью символов ##. Напомним, что одиночный символ # используется для однострочного комментария, т.е. предикат можно рассматривать как предельно точный и четкий комментарий.
Глава 2. Процессы и синхронизация 63
Цель логики программирования состоит в том, чтобы обеспечить возможность обосновывать (доказывать) свойства выполнения программы. Следовательно, интерпретация тройки характеризует отношение между предикатами {Р} и {Q} и списком операторов S.
(2.4) Интерпретация тройки. Тройка {Р} S {Q} истинна при условии, что если выполнение S начинается в состоянии, удовлетворяющем Р, и завершается, то результирующее состояние удовлетворяет Q.
Эта интерпретация называется частичной корректностью, которая является свойством безопасности в соответствии с определением из раздела 2.1. Она утверждает, что если начальное состояние программы удовлетворяет Р, то заключительное состояние будет удовлетворять Q при условии, что выполнение S завершится. Соответствующее свойство живучести — это тотальная (полная) корректность, т.е. частичная корректность плюс завершимость (все истории конечны).
Предикаты Р и Q в тройке часто называются утверждениями, поскольку они утверждают, что состояние программы должно удовлетворять предикату, чтобы интерпретация тройки была истинной. Таким образом, утверждение характеризует допустимое состояние программы.
Предикат Р называется предусловием S. Он описывает условие, которому должно удовлетворять состояние перед началом выполнения S. Предикат Q называется постусловием S. Он описывает состояние после выполнения S при условии, что выполнение S завершается. Двумя особыми утверждениями являются true (истина), характеризующее все состояния программы, и false (ложь), которое не описывает ни одного состояния программы.
Для того чтобы интерпретация (2.4) была моделью нашей логики программирования, аксиомы и правила вывода ЛП должны быть непротиворечивыми относительно (2.4). Это гарантирует, что все доказуемые в ЛП теоремы непротиворечивы. Например, такая тройка должна быть теоремой:
{х == 0} х = х+1; {х == 1}
Однако следующая тройка не будет теоремой, поскольку присваивание значения переменной х не может чудесным образом изменить значение у на 1:
{х == 0} х = х+1; {у == 1}
В дополнение к непротиворечивости логика должна быть (относительно) полной, чтобы истинные тройки в действительности были доказуемыми теоремами.
Важнейшей аксиомой логики программирования, такой как ЛП, является аксиома, связанная с присваиванием.
Аксиома присваивания. {Рх <_ е} х = е {Р}
Запись Рх <_ е определяет текстуальную подстановку: заменить все свободные вхождения переменной х в предикат Р выражением е. (Переменная является свободной в предикате, если она не входит в область действия квантора существования или всеобщности, имеющего переменную с тем же именем.) Аксиома присваивания гласит, что если нужно, чтобы присваивание приводило к состоянию, удовлетворяющему предикату Р, то предшествующее состояние должно удовлетворять предикату Р, в котором вместо переменной х записано выражение е. В качестве примера для этой аксиомы приведем следующую тройку: {1 == 1} х = 1; {х == 1}
Предусловие упрощается до предиката true, характеризующего все состояния. Таким образом, эта тройка означает, что, независимо от начального состояния, после присваивания х значения 1 получается состояние, удовлетворяющее предикату х == 1.
Более общий способ рассматривать присваивание — "идти вперед", т.е. начать с некоторого предиката, характеризующего текущее состояние, а затем записать предикат, истинный для состояния после выполнения присваивания. Например, если начать в состоянии, в котором х == О, и прибавить 1 к х, то в результирующем состоянии значением х будет 1. Это описывается тройкой {х == 0} х = 1; {х == 1}.
64 Часть 1. Программирование с разделяемыми переменными
Аксиома присваивания описывает изменение состояния. Правила вывода в такой логике программирования, как ЛП, позволяют сочетать теоремы, полученные из частных случаев аксиомы присваивания. В частности, правила вывода используются для описания действия композиции операторов (списков операторов) и управляющих операторов, например if и while. Они также позволяют изменять предикаты в тройках.
На рис. 2.1 представлены четыре наиболее важных правила вывода. Правило композиции позволяет склеить тройки для двух операторов, выполняемых один за другим. Первая гипотеза в правиле оператора if характеризует результат выполнения оператора s, когда условие В истинно; вторая описывает, что является истинным, когда в ложно; заключение объединяет эти два случая. В качестве простого примера использования этих правил рассмотрим программу, которая присваивает переменной m максимальное из значений х и у.

Для правила оператора while требуется инвариант цикла I. Это предикат, значение которого истинно перед каждым повторением цикла и после него. Если инвариант I и условие цикла в истинны перед выполнением тела цикла S, то выполнение S должно снова сделать I истинным. Таким образом, когда оператор цикла завершается, инвариант I остается истинным, а В становится ложным. В качестве примера приведем следующую программу, которая просматривает массив а и ищет в нем первое вхождение значения х. При условии, что х встречается в а, цикл завершается присвоением переменной i индекса первого вхождения.
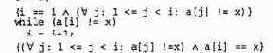
Здесь инвариантом цикла является предикат с квантором. Он истинен перед выполнением цикла, поскольку область определения квантора пуста. Он также истинен перед каждым вы-
Глава 2 Процессы и синхронизация 65
полнением тела цикла и после него. Когда выполнение оператора цикла завершается, а [ i ] равно х, и х ранее не встречался в массиве а.
Правило следования позволяет усиливать предусловия и ослаблять постусловия. В качестве примера рассмотрим истинную тройку:
{х = = 0} х = х+1; {х = = 1). По правилу следования истинной будет и такая тройка:
{х = = 0} х = х+1; {х > 0}.
Во второй тройке постусловие слабее, чем в первой, поскольку оно характеризует больше состояний; значение х может как равняться 1, так и вообще быть неотрицательным.
2.6.3. Семантика параллельного выполнения
Оператор параллельного выполнения со (или объявление процесса) является управляющим оператором. Следовательно, его действие описывается правилом вывода, учитывающим воздействие параллельного выполнения. Процессы состоят из последовательных операторов и операторов синхронизации, таких как оператор await.
С точки зрения частичной корректности действие оператора await
(await (В) S;>
больше всего похоже на действие оператора if, для которого условие в истинно, когда начинается выполнение S. Следовательно, правило вывода для оператора await аналогично правилу вывода для оператора if.
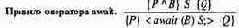
Гипотеза гласит: "если выполнение S начинается в состоянии, когда и Р, и В истинны, и S завершается, то Q будет истинным". Заключение позволяет сделать вывод о том, что оператор await приводит к состоянию, удовлетворяющему Q, если начинается в состоянии, удовлетворяющем Р (при условии, что выполнение оператора await завершается). Правила вывода ничего не говорят о возможных задержках выполнения, поскольку задержки влияют на свойства живучести, а не на свойства безопасности.
Теперь рассмотрим влияние параллельного выполнения, заданного, например, таким оператором:
со Si; // S2; // ... // Sn; ос; Предположим, что для каждого оператора истинно следующее выражение:
{Р,} S1 {Q,}
В соответствии с интерпретацией троек (2.4) это означает, что если зх начинается в состоянии, удовлетворяющем р!, и зх завершается, то состояние удовлетворяет qi. Для того чтобы эта интерпретация оставалась верной при параллельном выполнении, процессы должны начинаться в состоянии, удовлетворяющем конъюнкции предикатов Pi. Если все процессы завершаются, заключительное состояние будет удовлетворять конъюнкции предикатов ql Таким образом, получается следующее правило вывода.
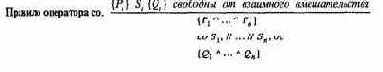
66 Часть 1. Программирование с разделяемыми переменными
Отметим фразу в гипотезе. Чтобы заключение было истинным, процессы и их обоснования не должны влиять друг на друга.
Один процесс вмешивается в другой (влияет на другой), если он выполняет присваивание, нарушающее утверждение в другом процессе. Утверждения характеризуют, что в процессе предполагается истинным до и после выполнения каждого оператора. Таким образом, если один процесс присваивает значение разделяемой переменной и тем самым делает недействительным предположение другого процесса, то обоснование другого процесса становится ложным. В качестве примера рассмотрим следующую простую программу: {х == 0}
со (х = х+1;} // <х = х+2;} ос {х == 3}
Если выполнение программы начинается состоянием, в котором значение х равно 0, то при завершении программы значение х будет равно 3. Но что же будет истинным для каждого процесса? Нельзя предполагать, что значение х будет 0 в начале каждого из них, поскольку порядок выполнения операторов недетерминирован. В частности, на предположение, что в начале выполнения процесса х имеет значение 0, влияет другой процесс, если выполняется первым. Однако то, что является истинным, учитывается следующими утверждениями.
Глава 2. Процессы и синхронизация 67
В качестве примера использования (2.5) рассмотрим последнюю из приведенных выше программ. Предусловие первого процесса является критическим утверждением. На него не влияет оператор присваивания во втором процессе, поскольку истинна такая тройка:
{ (х == 0 v х == 2) л (х == 0 v х == 1)}
х = х+2;
{х == 0 v х == 2}
Первый предикат упрощается до х == 0, поэтому после прибавления 2 к х значение переменной х будет или 0, или 2. Эта тройка выражает следующий факт: если второй процесс выполняется перед первым, то в начале выполнения первого процесса переменная х будет иметь значение 2. В данной программе есть еще три критических утверждения: постусловие первого процесса, пред- и постусловие второго процесса. Все доказательства взаимного невмешательства аналогичны приведенному.