Матричные вычисления
Сеточные и точечные вычисления являются фундаментальными в научных вычислениях. Третий основной вид вычислений — матричные. Умножение плотных и разреженных матриц уже рассматривалось. В данном разделе представлено использование матриц для решения систем линейных уравнений. Задачи такого типа составляют основу многих научных и инженерных приложений, а также задач экономического моделирования и многих других. (В действительности уравнение Лапласа, рассмотренное в разделе 11.1, можно заменить большой системой уравнений. Однако эта система получится очень разреженной, поэтому уравнение Лапласа обычно решают с помощью итерационных сеточных вычислений.)
Вначале рассмотрен метод исключений Гаусса. Затем описан более общий метод, который называется LU-разложением, и для него построена последовательная программа. Наконец разработаны параллельные программы для LU-разложения с разделяемыми переменными и с передачей сообщений. В упражнениях представлены другие матричные вычисления, в том числе обращение матриц.

Стандартный способ решения данной системы с неизвестными а, Ь и с — переписать одно из уравнений относительно какой-либо переменной, скажем, а, и полученное для нее выражение подставить в два других уравнения. Получим два новых уравнения с двумя неизвестными. ' Затем выполним с ними те же действия — перепишем одно уравнение относительно одной из переменных, скажем, Ь, и подставим полученное для b выражение во второе уравнение. Решим полученное уравнение относительно с, затем найдем Ь и, наконец, а.
Метод (процедура) исключений Гаусса является систематическим методом решения систем линейных уравнений любых размеров. Для указанных выше трех уравнений он работает следующим образом. Первый шаг: умножим первое уравнение на 2 и вычтем его из второго. Из второго уравнения исключается а. Второй шаг: умножим первое уравнение на -1 и вычтем его из третьего (т.е. сложим первое и третье уравнения); а исключается из третьего уравнения. Итак, получены уравнения

Глава 11. Научные вычисления 437
Повторим описанные выше действия для двух последних уравнений. Умножим второе уравнение на 2/3 и сложим его с третьим. В третьем уравнении исчезает Ь (и появляется с). Получается система уравнений
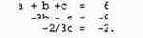
Описанные выше действия систематически исключают одну переменную из оставшихся уравнений и называются прямым ходом (фазой исключений). Во второй фазе выполняется обратный ход, в котором неизвестные находятся в обратном порядке, начиная с последнего уравнения и заканчивая первым. В нашем примере из последнего уравнения получим с = 3. Затем во второе уравнение вместо с подставим 3 и найдем значение b: b = 2. Наконец подставим полученные для b и с значения в первое уравнение и найдем а: а = 1. Итак, решение данной системы уравнений — а = 1,Ь = 2ис = 3.
Решение системы линейных уравнений эквивалентно решению матричного уравнения Ах = Ь, где а — квадратная матрица коэффициентов, b — вектор-столбец правых частей уравнений, ах— вектор-столбец неизвестных. Строка с номером i матрицы А содержит коэффициенты для неизвестных 1-го уравнения, а i-й элемент в столбце Ь— значение правой части 1-го уравнения.
Метод исключений Гаусса реализуется серией преобразований матрицы А и вектора Ь. Матрица А приводится к верхней треугольной матрице, у которой все элементы, расположенные ниже главной диагонали, равны нулю. В нашем примере начальное значение матрицы А таково:
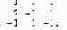
Соответствующие значения в Ь— (6, 3, -2). Прямой ход начинается с левого столбца и преобразует а и b следующим образом. Первый шаг: вычисляем множитель А[2,1]/А[1,1], умножаем на него первую строку матрицы А и первый элемент Ь; полученные строку и элемент вычитаем из второй строки А и второго элемента Ь. Второй шаг: вычисляем множитель А[3,1]/А[1,1], умножаем на него первую строку матрицы А и первый элемент Ь, и вычитаем их из третьей строки А и третьего элемента Ь. После этих двух шагов в первом столбце А будут нули во второй и третьей строках.
Последний шаг прямого хода в нашем несложном примере — вычисляем множитель А[3,2]/А[2,2], умножаем на него вторую строку А и второй элемент b и вычитаем их из третьей строки А и третьего элемента Ь. В итоге матрица А примет вид
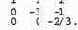
Соответствующие значения для b — (б, -9, -2).
Метод исключений Гаусса можно использовать при решении многих систем п уравнений с п неизвестными.23 Однако на каждом шаге прямого хода вычисляются множители вида A[k,i]/A[i,i]. Элемент А [ i, i ] называется ведущим элементом столбца i. Если он равен нулю, то получится "деление на ноль". Кроме того, если ведущий элемент слишком мал, то множитель будет слишком большим. Это может сделать алгоритм численно неустойчивым.
Обе проблемы можно решить, используя метод главных элементов. В каждом столбце i выбирается главный элемент A[k,i], имеющий наибольшее абсолютное значение. Перед следующим шагом исключений выполняется перестановка строк k и i. Ее лучше реализовать с помощью перестановки указателей на строки, а не путем реальных обменов значений их элементов.
" При этом уравнения должны быть независимыми, т.е. никакое уравнение системы не может быть получено из других. Точнее, А должна быть несингулярной (неособенной) матрицей.
438 Часть 3. Синхронное параллельное программирование
11.3.2. LU-разложение
Метод исключений Гаусса преобразует уравнение Ах = b в эквивалентное ему уравнение Ux = у, где и— верхняя треугольная матрица. При этом вычисляется последовательность множителей. Вместо того, чтобы отбрасывать их, предположим, что они сохраняются в третьей матрице L. Пусть матрица L — нижняя треугольная матрица, в которой все элементы, расположенные выше главной диагонали, равны нулю. Каждый элемент L [ j , i ] на диагонали и под ней имеет значение вида А [ j , i ] /pivot, где pivot — значение ведущего элемента для столбца i. После заполнения матрицы L произведение матриц L и и будет в точности равно исходной матрице А (если не учитывать возможных ошибок округления).
В частности, для нашей системы уравнений получим:
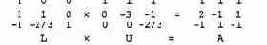



11.3.3. Программа с разделяемыми переменными
Рассмотрим, как распараллелить программы в листингах 11.11 и 11.12, используя pr процессоров и, соответственно, pr рабочих процессов. Вначале рассмотрим LU-разложение (см. листинг 11.11). В нем есть две фазы: инициализация ps и ш, а затем прямой ход исключений Гаусса. В фазе инициализации тела циклов независимы, поэтому их можно разделить
440 Часть 3. Синхронное параллельное программирование
между рабочими, используя любую схему распределения, которая каждому рабочему назначает поровну элементов данных.
Внешний цикл (по k) в фазе исключений должен выполняться последовательно каждым рабочим процессом, поскольку LU-разложение происходит итеративно вниз по главной диагонали и разлагает подматрицу LU[k:n,k:n]. Тело внешнего цикла имеет две фазы — выбор ведущего элемента и ведущей строки, затем сокращение строк под ведущей. Ведущий элемент можно выбрать следующими тремя способами.
• Каждый процесс просматривает все элементы в LU[k:n,k] и выбирает наибольший. Если каждый процесс сохраняет свою собственную копию индексов ведущих элементов ps, то после завершения этой фазы барьер не нужен.
• Один процесс просматривает все элементы в LU [ k: n, k ], выбирает наибольший и меняет местами ведущую строку и строку k. Здесь нужна точка барьерной синхронизации.
• Каждый рабочий процесс проверяет свое подмножество элементов из LU[k:n,k], выбирает наибольший элемент из подмножества и затем согласовывает с другими выбор ведущего элемента. Здесь также нужна точка барьерной синхронизации и в зависимости от того, как она запрограммирована, собственные копии ps.
Для малых значений n более быстрым будет первый подход, поскольку в нем нет барьеров. Для больших значений n более быстрым, вероятно, окажется третий подход. Точка пересечения (графиков сложности) зависит от того, как накладные расходы, связанные с барьером, соотносятся с временем выбора наибольшего элемента.
После выбора ведущего элемента все строки под ведущей строкой можно исключить параллельно. Для каждой строки сначала вычисляется и сохраняется множитель mult, затем выполняются итерации по столбцам, находящимся справа от столбца с ведущим элементом. По мере выполнения LU-разложения подматрица, в которой проводятся исключения, уменьшается, как и объем работы в фазах исключений. Таким образом, LU-матрицу нужно назначить рабочим процессам по полосам или обратным полосам, чтобы у каждого процесса постоянно была какая-то работа, кроме последних нескольких итераций в главном цикле. Вновь используем схему распределения по полосам, поскольку она проще программируется, чем схема с обратными полосами, и приводит к достаточно сбалансированной нагрузке.
В листинге 11.13 представлен эскиз параллельной программы LU-разложения с разделяемыми переменными. По сравнению с последовательной программой она имеет следующие основные отличия: 1) в фазах инициализации и исключений используются полосы строк; 2) после инициализации, каждой фазы выбора ведущего элемента (если необходимо) и каждого шага исключений установлены барьеры. Кроме того, каждому рабочему, возможно, нужна своя собственная локальная копия ведущих индексов, поскольку это упрощает перестановку строк и не требует синхронизации.


Рассмотрим, как распараллелить прямой и обратный проходы (см. листинг 11.12). К сожалению, в каждой фазе есть вложенные циклы, и каждый внутренний цикл зависит от значений, вычисленных на предыдущих итерациях соответствующего внешнего цикла. По определению прямой ход вычисляет элементы у по одному, а обратный — элементы х, также по одному.
В эти циклы можно внести независимость. Например, в фазе прямого хода можно развернуть внутренние циклы и переписать код, чтобы значения х [ i ] вычислялись в терминах ш и Ь. Вручную это делать утомительно, лучше использовать компилятор (см. раздел 12.2).
Другой способ получить параллельность — использовать так называемую синхронизацию фронта волны (wave front synchronization).
В фазе прямого хода итерации назначаются рабочим по полосам. Поскольку вычисления х [ i ] зависят от предыдущих значений х [ 1.- i -1 ], с каждым элементом х можно связать флаг (или семафор). Закончив вычисление х [ i ], процесс устанавливает флаг для этого элемента. Когда процессу нужно прочитать значение х [ i ], он сначала ждет, пока для этого элемента не будет установлен флаг. Например, код, выполняемый рабочим процессом w в прямом ходе, мог бы быть таким.

Фронт волны представляет собой установку флагов по мере вычисления новых элементов. (Термин фронт волны обычно используется для матриц; волна, как правило, представляет собой диагональную линию, движущуюся по матрице.)
Волновые фронты эффективны, если накладные расходы при синхронизации невелики по сравнению с объемом вычислений. Здесь же на каждый элемент приходится очень мало вычислений, поэтому синхронизацию можно запрограммировать с помощью простых флагов и активного ожидания. Это должно дать небольшое увеличение производительности данного приложения.
11.3.4. Программа с передачей сообщений
Рассмотрим, как реализовать LU-разложение с помощью передачи сообщений. Вновь рассмотрим три подхода — управляющий-рабочие, алгоритмы пульсации и конвейера. Можно использовать все три парадигмы, однако если в программе с разделяемыми переменными
442 Часть 3. Синхронное параллельное программирование
для некоторого приложения применяются барьеры, то естественнее всего построить распределенную программу на основе алгоритма пульсации. Ниже приведен эскиз программы пульсации для LU-разложения. Две другие парадигмы рассмотрены в упражнениях в конце главы.
Как обычно, при создании распределенной программы сначала нужно решить, как распределить данные, чтобы вычислительная нагрузка оказалась сбалансированной. Поскольку LU-разложение работает с уменьшающимися подматрицами, объем работы также уменьшается по мере выполнения исключений.
Поэтому можно назначить строки по полосам. Если предположить, что есть PR рабочих процессов, то рабочему процессу назначается каждая PR-я строка lu, по n/PR строк на каждый процесс.
Первый шаг в Ш-разложении — инициализация локальных строк ш и индексов ведущих элементов ps. Все процессы могут выполнить этот шаг параллельно. После инициализации барьер не нужен, поскольку здесь нет разделяемых переменных.
Главный шаг в LU-разложении — многократное повторение выбора ведущего элемента и ведущей строки с последующим исключением всех строк, расположенных ниже ведущей. Каждый рабочий процесс может выбрать наибольший элемент в столбце k своих n/PR строк в матрице lu. Однако для выбора глобального максимума рабочим нужно взаимодействовать. Можно использовать один процесс в качестве управляющего, который собирает максимальные значения от всех процессов, выбирает наибольшее из них и рассылает его копии. Или же, если доступны такие глобальные примитивы взаимодействия, как в библиотеке MPI, то для вычисления ведущего значения можно использовать примитив редукции.
После выбора ведущего значения процесс, которому принадлежит ведущая строка, должен передать ее другим, поскольку она им нужна в фазе исключения. Получив ведущие значение и строку, каждый рабочий процесс может выполнить исключение строк своей области под ведущей строкой.
В листинге 11.14 содержится эскиз программы с передачей сообщений для LU-разложения. Все шаги в программе такие, как описано выше. Явные барьеры здесь не нужны, поскольку обмен сообщениями, необходимый при выборе ведущего значения и ведущей строки, по сути, является барьером. В фазе исключений используется переменная myRow, чтобы отображать глобальный индекс i-й строки (который находится в диапазоне от 1 до п) в индекс соответствующей строки в локальном массиве строк.


Когда программа в листинге 11.14 завершается, результаты LU-разложения размещаются в локальных массивах рабочих процессов. Чтобы решить систему уравнений, нужно выполнить как прямой, так и обратный ход, т.е.
действия, требующие доступа ко всем элементам LU-разложения. Первый подход состоит в использовании процесса, который собирает все строки LU и затем выполняет код из листинга 11.12. При втором используется круговой конвейер, чтобы реализовать синхронизацию фронта волны с помощью передачи сообщений.
В круговом конвейере первый рабочий процесс вычисляет х [ 1 ] и передает его второму. Второй процесс вычисляет х [ 2 ] и передает х [ 2 ] и х [ 1 ] третьему. Последний процесс вычисляет х[ PR] и передает его и все предыдущие значения первому. Это продолжается до тех пор, пока не будет вычислен х [п]. Можно использовать такой же конвейер для обратного хода, вычисляя окончательные значения х[п],х[п-1] и так вплоть до х [ 1 ] и передавая их по конвейеру.
Конвейер для прямого и обратного хода относительно легко программируется, параллелен по существу и не требует сбора всех элементов Ш. Однако ему нужно много сообщений, поэтому вполне вероятно, что он может оказаться менее эффективным, чем алгоритм с одним процессом.