Конвейерные алгоритмы
Напомним, что процесс-фильтр получает данные из входного порта, обрабатывает их и отсылает результаты в выходной порт. Конвейер — это линейно упорядоченный набор процессов-фильтров. Данная концепция уже рассматривалась в виде каналов Unix (раздел 1.6), сортирующей сети (раздел 7.2), а также как способ циркуляции значений между процессами (раздел 7.4). Здесь показано, что эта парадигма полезна и в синхронных параллельных вычислениях.
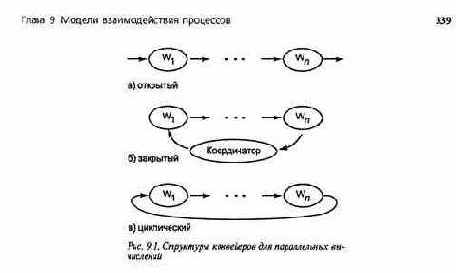
В решении задач параллельных вычислений обычно используется несколько рабочих процессов. Иногда их можно программировать в виде фильтров и соединять в конвейер параллельных вычислений. Есть три базовые структуры таких конвейеров (рис. 9.1): открытая, закрытая и циклическая (круговая). Рабочие процессы обозначены символами от Wt до Wf В открытом конвейере входной источник и выходной адресат не определены. Такой конвейер можно включить в любую цепь, для которой он подходит. Закрытый конвейер — это открытый конвейер, соединенный с, управляющим процессом, который производит входные данные для первого рабочего процесса и потребляет результаты, вырабатываемые последним рабочим процессом. Пример открытого конвейера — команда Unix "grep pattern file | we", которую можно поместить в самые разные места. Выполняясь в командной строке, эта команда становится частью закрытого конвейера с пользователем в качестве управляющего процесса. Конвейер называется циклическим (круговым), если его концы соединены; в этой ситуации данные циркулируют между рабочими процессами.
В разделе 1.8 были представлены две распределенные реализации умножения матриц а х Ь = с, где а, Ь и с — плотные матрицы размерами n x п. В первом решении работа просто делилась между n рабочими процессами, по одному на строку матриц а и с, но каждый процесс должен был хранить всю матрицу Ь. Во втором решении также использовались n рабочих процессов, но каждый из них должен был хранить только один столбец матрицы Ь. В этом решении в действительности применялся круговой конвейер, в котором между рабочими процессами циркулировали столбцы матрицы Ь.
Здесь будут рассмотрены еще две распределенные реализации умножения плотных матриц. В первом решении используется закрытый конвейер, во втором — сеть циклических конвейеров. Оба решения имеют интересные особенности по сравнению с рассмотренными ранее алгоритмами, они также демонстрируют шаблоны, применимые к другим задачам.

340 Часть 2 Распределенное программирование
чения а [ i, * ]. Во второй фазе рабочие процессы получают столбцы матрицы Ь, сразу передают их следующему рабочему процессу и вычисляют одно промежуточное произведение. Эту фазу каждый рабочий процесс повторяет п раз, получая в результате значения с [ i, * ]. В третьей фазе каждый рабочий процесс отсылает свою строку матрицы с следующему рабочему процессу, затем получает и передает далее строки матрицы с от предшествующих процессов конвейера. Последний рабочий процесс передает свою и остальные полученные строки матрицы с управляющему. При этом строки передаются в порядке от с[п-1,*] до с [ 0, * ], поскольку в этом порядке их получает последний рабочий процесс конвейера. При таком порядке передачи снижаются задержки взаимодействия, а последнему рабочему процессу не нужна локальная память для хранения всей матрицы с.
Действия рабочих процессов показаны в листинге 9.5, б. Три фазы работы процессов отмечены комментариями. Учтены отличия последнего рабочего процесса от остальных.

Глава 9. Модели взаимодействия процессов 341
ния идут непрерывно. Вычисляя промежуточное произведение, рабочий процесс уже передал используемый столбец, поэтому следующий процесс может его получить, передать дальше и начать вычисление своего собственного промежуточного произведения.
Во-вторых, чтобы первый рабочий процесс получил все строки матрицы а и передал их далее, нужно n циклов передачи сообщений. Еще п-1 циклов нужно, чтобы заполнить конвейер, т.е.
чтобы каждый рабочий процесс получил свою строку матрицы а. Однако после заполнения конвейера промежуточные произведения вычисляются почти с той же скоростью, с какой могут приходить сообщения. Причина, как уже отмечалось, в том, что столбцы матрицы Ь следуют сразу за строками матрицы а и передаются рабочими процессами сразу после получения. Если вычисление промежуточного произведения занимает больше времени, чем передача и прием сообщения, то после заполнения конвейера определяющим фактором станет время выполнения вычислений. Оставляем читателю решение интересных задач по выводу уравнений производительности и проведение опытов с пропускной способностью конвейера.
Еще одно интересное свойство рассматриваемого решения — возможность легко изменять число столбцов матрицы Ь. Для этого достаточно изменить верхние пределы в циклах обработки столбцов. Фактически такой же код можно использовать для умножения матрицы а на любой поток векторов, чтобы получить в результате поток векторов. Например, матрица а может представлять набор коэффициентов линейных уравнений, а поток векторов — различные комбинации значений переменных.
Конвейер также можно "сократить", чтобы использовать меньше рабочих процессов. Для этого каждый рабочий процесс должен хранить полосу строк матрицы а. Можно точно так же передавать по конвейеру столбцы матрицы Ь и строки с или, уменьшив количество сообщений, сделать их длиннее.
Закрытый конвейер, показанный в листинге 9.5, можно открыть и поместить его рабочие процессы в цепочку другого конвейера. Например, вместо управляющего процесса для соз-чания исходных векторов можно использовать еще один конвейер умножения матриц, а для юлучения результатов — еще один процесс. Однако, чтобы придать конвейеру наиболее об-ций вид, через него нужно передавать все векторы (даже строки матрицы а) — тогда на выхо-(е из конвейера эти данные будут доступны какому-нибудь другому процессу.
J.3.2. Блочное умножение матриц
Производительность предыдущего алгоритма определяется длиной конвейера и временем, «обходимым для передачи и приема сообщений.
Сеть связи некоторых высокопроизводитель-шх машин организована в виде двухмерной сетки или структуры, которая называется гиперкубом. Эти виды сетей связи позволяют одновременно передавать сообщения между различными парами соседствующих процессов. Кроме того, они уменьшают расстояние между процессора-пи по сравнению с их линейным упорядочением, что сокращает время передачи сообщения.
Для эффективного умножения матриц на машинах с такими структурами сети связи нужно делить матрицы на прямоугольные блоки и для обработки каждого блока использовать отдельный рабочий процесс. Таким образом, рабочие процессы и данные распределяются по процессорам в виде двухмерной сетки. У каждого рабочего процесса есть по четыре соседа: сверху, снизу, слева и справа. Соседями считаются рабочие процессы в верхнем и нижнем рядах сетки, а также в ее левом и правом столбцах.
Вернемся к задаче вычисления произведения двух матриц а и Ь с размерами n x n и сохранения результата в матрице с. Чтобы упростить код, используем отдельный рабочий процесс для каждого элемента матрицы и пронумеруем строки и столбцы от 1 до п. (В конце раздела описано использование блоков значений.) Пусть массив Worker [ 1.- n, 1.- n ] — это матрица рабочих процессов. Матрицы а и Ь вначале распределены так, что у каждого процесса Worker [ i, j ] есть соответствующие элементы матриц а и Ь.
342 Часть 2. Распределенное программирование
Для вычисления с I i, j ] рабочему процессу Worker [ i, j ] нужно умножить каждый элемент строки i матрицы а на соответствующий элемент столбца j матрицы b и сложить результаты. Однако порядок выполнения операций умножения на результат не влияет! Вопрос в том, как организовать циркуляцию данных между рабочими процессами, чтобы каждый из них получил все необходимые пары чисел.
Для начала рассмотрим процесс Worker [1,1]. Для вычисления значения с [ 1,1 ] этому процессу нужны все элементы строки 1 матрицы а и столбца 1 матрицы Ь.
Вначале у процесса есть а[1,1] и Ь [ 1,1 ], поэтому их можно сразу перемножить. Если теперь переместиться на 1 вправо по строке матрицы а и вниз по столбцу матрицы Ь, то процесс Worker [1,1] получит значения элементов а[1,2] и Ь[2,1 ], которые можно умножить и прибавить к значению с [ 1,1 ]. Если эти действия повторить еще п-2 раза, перемещаясь вправо по строке матрицы а и вниз по столбцу матрицы Ь, то процесс Worker [1,1] получит все необходимые ему данные.
К сожалению, такая последовательность сдвигов и умножений годится только для процесса, обрабатывающего диагональные элементы матрицы. Другие рабочие процессы тоже увидят необходимые им значения элементов матриц, но в неправильной последовательности. Однако перед началом умножений и перемещений элементы матриц а и Ь можно переупорядочить. Для этого нужно сначала циклически сдвинуть строку i матрицы а влево на i столбцов, а столбец j матрицы Ь вверх на j строк. (Причины, по которым такое перемещение элементов работает, не очевидны; этот порядок перемещения элементов был получен после исследований, проведенных для небольших матриц, и обобщения результатов.) Ниже показан результат предварительной перестановки значений матриц а и Ь с размерами 4x4. ai,2, b2,i ai,3, Ьз,2 ai,4, bi,3 ai,i, bi,i
32,3, Ьз,1 32,4, bt,2 32,1/ t>l,3 32,2. Ь2,4
аз,4, b4,i аз,1, bi,2 аз,2, Ь2,з аз,з, Ьз,4
a4,i, bi.i 34,2, Ь2,2 а4,з, Ьз,з а4,4, Ьа,4
После предварительной перестановки значений каждый рабочий процесс имеет два значения, которые он записывает в локальные переменные aij и bij. Затем рабочий процесс инициализирует переменную cij значением aij *bij и выполняет п-1 циклов сдвига и умножения. В каждом цикле значения aij передаются на один столбец влево, а значения bij — на строку выше; процесс получает новые значения, перемножает их и прибавляет произведение к текущему значению переменной cij.
Когда рабочие процессы завершаются, произведение матриц хранится в переменных cij всех рабочих процессов.
В листинге 9.6 показан код, реализующий этот алгоритм умножения матриц. Рабочие процессы совместно используют п2 каналов для циркуляции данных влево и еще п2 каналов для циркуляции данных вверх. Из каналов формируются 2п пересекающихся циклических конвейеров. Рабочие процессы одной строки связаны в циклический конвейер, через который данные перемещаются влево; рабочие процессы одного столбца связаны в циклический конвейер, по которому данные идут вверх. Константы LEFT1, UP1, LEFTI и UPJ в каждом рабочем процессе инициализируются соответствующими значениями и используются в операторах send для индексации массивов каналов.

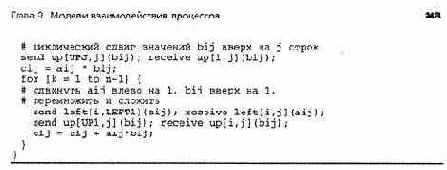
программа в листинге у.о явно неэффективна (если только она не реализована аппарат-но). В ней используется слишком много процессов и сообщений, а каждый процесс производит слишком мало вычислений. Но этот алгоритм легко обобщается для использования квадратных или прямоугольных блоков. Каждый рабочий процесс назначается для блоков матриц а и Ь Рабочие процессы сначала сдвигают свои блоки матрицы а влево на i блоков столбцов, а блоки матрицы Ь — вверх на j блоков строк. Затем каждый рабочий процесс инициализирует свой блок результирующей матрицы с промежуточными произведениями своих новых блоков матриц а и Ь. Затем рабочие процессы выполняют п-1 циклов сдвига матрицы а на блок влево и сдвига матрицы Ь на блок вверх, вычисляют новые промежуточные произведения и прибавляют их к с. Подробности этого процесса читатель может выяснить самостоятельно (см. упражнения в конце главы).
Дополнительный способ повысить эффективность кода в листинге 9.6 — выполнять при сдвиге данных оба оператора send до выполнения операторов receive. Изменим последовательность операторов
send/receive/send/receive на
send/send/receive/receive.
Это снижает вероятность того, что оператор receive заблокирует работу программы, и делает возможной параллельную передачу сообщений (если она обеспечена сетью связи).