Алгоритмы типа "зонд-эхо"
Во многих приложениях, таких как Web-поиск, базы данных, игры и экспертные системы, используются деревья и графы. Особое значение они имеют для распределенных вычислений, многие из которых имеют структуру графа с узлами-процессами и ребрами-каналами.
Поиск в глубину (Depth-first search — DPS) — один из классических алгоритмов последовательного программирования для обхода всех узлов дерева или графа. Стратегия DFS в дереве-для каждого узла дерева посетить его узлы-сыновья и после этого вернуться к родительскому узлу. Этот вид поиска называется "поиск в глубину", поскольку каждый путь поиска сначала доходит вниз до узла-листа и лишь затем поворачивает; например, первым будет пройден путь от корня дерева к его крайнему слева листу. В графе общего вида, у которого могут быть циклы, используется тот же подход, нужно только помечать уже пройденные узлы, чтобы проходить по ребрам, выходящим из узла, только по одному разу.
В этом разделе описана парадигма (модель) "зонд-эхо" для распределенных вычислений в графах. Зонд — это сообщение, передаваемое узлом своему преемнику; эхо — последующий ответ. Поскольку процессы выполняются параллельно, зонды передаются всем преемникам также параллельно. Модель "зонд-эхо", таким образом, является параллельным аналогом модели DFS. Сначала модель зонда будет проиллюстрирована на примере рассылки информации всем узлам сети. Затем при разработке алгоритма построения топологии сети будет добавлено понятие эха.
344 Часть 2. Распределенное программирование
9.4.1. Рассылка сообщений в сети
Предположим, что есть сеть узлов (процессоров), связанных двунаправленными каналами связи. Узлы могут напрямую связываться со своими соседями. Сеть, таким образом, имеет структуру неориентированного графа.
Предположим, что один узел-источник S должен разослать сообщение всем узлам сети. (Точнее, процессу, выполняемому на узле S, нужно разослать сообщение процессам, выполняемым на всех остальных узлах.) Например, на узле s может выполняться сетевой управляющий процесс, которой должен передать новую информацию о состоянии всем остальным узлам.
Если все остальные узлы являются соседями S, рассылка сигнала реализуется тривиально: узел S должен просто напрямую отправить сообщение каждому узлу. Однако в больших сетях узел обычно имеет лишь небольшое количество соседей. Узел S может послать сообщение соседям, а они в свою очередь должны будут передать его своим соседям и так далее. Итак, нам нужен способ рассылки зонда всем узлам.
Предположим, что узел S имеет локальную копию топологии сети. (Позже будет показано, как ее вычислить.) Топология представлена симметричной матрицей логических значений, ее элемент topology [ i, j ] имеет значение "истина", если узлы i и j соединены, и "ложь" — в противном случае.
Для эффективной рассылки сообщения узел S должен сначала создать остовное дерево сети с собой в качестве корня этого дерева. Остовное дерево графа — это дерево, в которое входят все узлы графа, а ребра образуют подмножество ребер графа. На рис. 9.2 показан пример такого дерева; узел S находится слева. Сплошными линиями обозначены ребра остовного дерева, а пунктирными — остальные ребра графа.
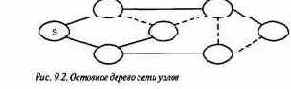
По данному остовному дереву t узел S может разослать сообщение т, передав его вместе с t всем своим сыновним узлам. Получив сообщение, каждый узел просматривает дерево t, чтобы определить свои сыновние узлы, после чего передает им всем сообщение m и дерево t. Остовное дерево передается вместе с сообщением т, поскольку иначе все узлы, кроме S, не будут знать, какое дерево использовать. Полный алгоритм приведен в листинге 9.7. Поскольку t — остовное дерево, в конце концов сообщение попадет во все узлы. Кроме того, каждый узел получит сообщение только один раз от своего родительского узла в дереве t. Для запуска рассылки сообщения используется отдельный процесс initiator в узле S, благодаря чему процессы Node на всех узлах идентичны.


346 Часть 2. Распределенное программирование
По алгоритму рассылки с помощью остовного дерева передается п-1 сообщений — по одному на каждое ребро между родительским и сыновним узлами остовного дерева.
По алгоритму, использующему множества соседей, через каждую связь сети нужно передать два сообщения, по одному в каждом направлении. Точное число сообщений зависит от топологии сети, но в общем случае оно будет намного больше, чем п-1. Например, если топология сети представляет собой дерево, в корне которого находится узел-источник, будут переданы 2 (п-1) сообщений. Для полного графа, в котором есть связи между всеми узлами, потребуется п (п-1) сообщений. Однако в алгоритме с множествами соседей узлу-источнику не нужно знать топологию сети или строить остовное дерево. По существу, остовное дерево строится динамически, оно состоит из связей, по которым проходят первые копии сообщения т. Кроме того, в этом алгоритме сообщения короче, поскольку в каждом из них не нужно передавать остовное дерево.
Оба алгоритма рассылки сообщений предполагают, что топология сети не меняется. Однако они не будут работать правильно, если во время их выполнения даст сбой один из процессоров или одна из связей. Если поврежден узел, он не сможет получить рассылаемое сообщение, а если — линия связи, могут стать недоступными связанные с ней узлы. Работы, в которых рассматриваются проблемы реализации отказоустойчивой рассылки сообщений, описаны в исторической справке в конце главы.
9.4.2. Построение топологии сети
Для применения эффективного алгоритма рассылки сообщений (см. листинг 9.7) необходимо заранее знать топологию сети. Здесь показано, как ее построить. Вначале каждому узлу известна лишь его локальная топология, т.е. связи с соседями. Задача в том, чтобы собрать воедино все локальные топологии, поскольку их объединение является общей топологией сети.
Топология собирается в две фазы. Сначала каждый узел посылает зонд своим соседям, как это происходило в листинге 9.8. Затем каждый узел отсылает эхо, содержащее информацию о локальной топологии, тому узлу, от которого он получил первый зонд. В конце концов инициирующий узел собирает все ответы-эхо и, следовательно, всю топологию.
Затем он может, например, построить остовное дерево и разослать топологию всем остальным узлам.
Вначале предположим, что топология сети ациклична. Сеть является неориентированным графом, поэтому ее структура — дерево. Пусть узел S — это корень дерева и инициирующий узел. Тогда топологию можно собрать следующим образом. Сначала узел S передает зонды всем своим сыновним узлам. Когда эти узлы получают зонд, они передают его своим сыновним узлам и т.д. Таким образом, зонды распространяются по всему дереву и в конце концов достигают его листьев. Поскольку у листьев нет сыновних узлов, начинается фаза эха. Каждый лист отсылает эхо, содержащее множество соседних узлов, своему родительскому узлу. После получения эха от всех сыновей узел объединяет эти ответы со своим собственным множеством соседей и передает полученные данные своему родительскому узлу. В конце концов корневой узел получит эхо от каждого из своих сыновей. Объединение этих данных будет содержать всю топологию сети, поскольку начальный сигнал достигнет каждого узла, а каждый эхо-ответ содержит множество, состоящее из отвечающего узла, всех его соседей и их потомков.
Полный алгоритм "зонд-эхо" для^ сбора топологии сети в дереве приведен в листинге 9.9. Фаза зонда, по существу, является алгоритмом рассылки сообщения из листинга 9.8, за исключением того, что сообщения-зонды идентифицируют отправителя. Фаза эха возвращает информацию о локальной топологии вверх по дереву. Алгоритмы узлов не вполне симметричны, поскольку экземпляр процесса Nodetp], выполняемый в узле S, должен знать, что нужно отослать эхо процессу-инициатору.
Листинг 9.9. Алгоритм "зонд-эхо" для сбора топологии дерева
type graph = bool [n,n];
chan probe[n](int sender);
chan echo[n](graph topology) # фрагменты топологии
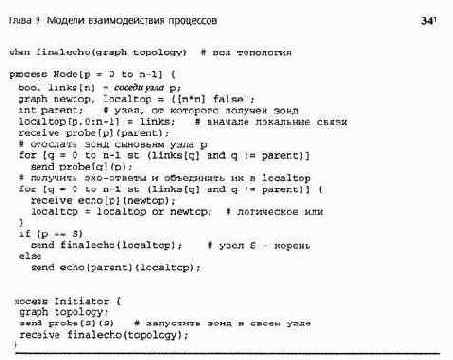
Для построения топологии сети с циклами рассмотренный алгоритм обобщается следую-дам образом. Получив зонд, узел передает его остальным своим соседям и ждет от них эха.
Однако, поскольку в сети есть циклы, а узлы работают параллельно, два соседа могут отослать зонды друг другу почти одновременно. На все зонды, кроме первого, эхо может быть отправлено немедленно. Если узел получает последующие зонды во время ожидания эха, он сразу отсылает эхо с пустой топологией (этого достаточно, поскольку локальные связи узла будут содержаться в эхе-ответе на первый зонд). В конце концов узел получит эхо в ответ на каждый зонд и передает эхо узлу, от которого получил первый зонд. Эхо содержит объединение данных о связях узла вместе со всеми остальными полученными данными.
Обобщенный алгоритм "зонд-эхо" построения топологии сети показан в листинге 9.10. Поскольку узел может получать последующие зонды во время ожидания эха, в один канал объединяются два типа сообщений. (Если бы они приходили по разным каналам, узлу нужно было использовать оператор empty и проводить опрос, чтобы решить, какой тип сообщения принять. Можно было бы использовать рандеву, выделив зонды и эхо в отдельные операции.) Корректность алгоритма вытекает из следующих фактов. Поскольку сеть является связной, каждый узел рано или поздно получит зонд. Взаимоблокировка не возникает, поскольку на каждый зонд посылается эхо-ответ (на первый зонд — перед завершением процесса Node, на остальные — сразу после их получения). Это позволяет избежать буферизации исходящих сообщений в каналах probe_echo. Последнее эхо, переданное узлом, содержит локальный набор соседей. Следовательно, объединение множеств соседей в конце концов достигает процесса Node [ S ], передающего топологию процессу initiator. Как и в листинге 9.8, связи, по которым проходят первые зонды, образуют динамически создаваемое остовное дерево. Топология сети возвращается вверх по остовному дереву; эхо от каждого узла содержит топологию поддерева, корнем которого является этот узел.
