Алгоритмы пульсации

Модель портфеля задач полезна для решения задач, которые возникают при использова­нии стратегии "разделяй и властвуй" или требуют фиксированного числа независимых задач. Парадигму пульсации можно применять во многих итерационных приложениях, параллельных по данным. Например, ее можно использовать, когда данные разделяются между рабочими процессами, каждый из которых отвечает за изменение определенной части данных, причем но­вые значения зависят от данных из этой же части или непосредственно прилегающих частей. Среди таких приложений — сеточные вычисления, возникающие при обработке изображений или решении дифференциальных уравнений в частных производных, и клеточные автоматы, используемые при моделировании таких процессов, как лесной пожар или биологический рост. Предположим, что есть массив данных. Каждый рабочий процесс отвечает за определен­ную часть данных и строится по следующей схеме.

process worker[w =  1  to numWorkers]   { декларации локальных переменных; инициализация локальных переменных; wh i 1 е   (не выполнено)   { send значения соседям; receive значения от соседей; обновить локальные значения; } }

334                                                                            Часть 2. Распределенное программирование

Этот тип межпроцессного взаимодействия называется алгоритмом пульсации, поскольку дей­ствия рабочих процессов напоминают работу сердца: расширение при отправке информации, сокращение при сборе новой информации, затем обработка информации и повторение цикла.

Если данные образуют двухмерную сетку, их можно разделить на полосы или блоки. При делении на полосы получим вектор рабочих процессов, у каждого из которых (кроме двух крайних) будет по два соседа. При делении на блоки получим матрицу рабочих процессов, и у каждого из них будет от двух до восьми соседей, в зависимости от положения блока в мас­сиве данных (внутри, на границе или в углу) и количества соседних значений, необходимых для обновления значений в блоке.
Трехмерные массивы данных можно делить аналогичным образом на плоскости, прямоугольные призмы или кубы.

Взаимодействие по схеме send-receive в алгоритме пульсации приводит к появлению "нечеткого" барьера между рабочими процессами. Напомним, что барьер — это точка син­хронизации, которой должны достичь все рабочие процессы перед тем, как продолжить рабо­ту. В итерационных вычислениях барьер не позволяет начать новую итерацию, пока все рабо­чие процессы не закончат предыдущую. Чтобы новая фаза обновления значений не начина­лась до того, как все процессы завершат предыдущую фазу, используется обмен сообщениями. Рабочие процессы, которые не являются соседями, могут порознь проводить больше одной итерации, но для соседних процессов это запрещено. Настоящий барьер здесь не нужен, поскольку рабочие процессы разделяют данные только со своими соседями.

Далее разрабатываются алгоритмы пульсации для двух задач: выделения областей (пример обработки изображений) и игры "Жизнь" (пример клеточного автомата). Дополнительные примеры приложений есть в упражнениях и в главе 11.

9.2.1. Обработка изображений: выделение областей

Изображение — это представление картинки; обычно оно состоит из матрицы чисел. Эле­мент изображения называется пикселем (от англ, picture element — pixel, элемент картины), и его значение представляет собой интенсивность света или цвет.

Существует множество операций обработки изображений, и каждая из них может выиг­рать от распараллеливания. Более того, одна и та же операция иногда применяется к потоку изображений. Операции обработки изображений бывают точечными (работают с отдельными пикселями, как, например, при контрастировании), локальными (обрабатывают группы пик­селей, как при сглаживании или подавлении шумов) и глобальными (над всеми пикселями, например, при кодировании или декодировании).

Рассмотрим локальную операцию, которая называется выделением областей. Пусть изо­бражение представлено матрицей image [m, n] целых чисел.


Для простоты предположим, что каждый пиксель имеет значение 1 (освещено) или 0 (не освещено). Его соседями считаются пиксели, расположенные сверху, снизу, слева и справа. (У пикселей в углах изображения по два соседа, на границах — по три.)

Задача выделения области состоит в поиске областей освещенных пикселей и присвоении каждой найденной области уникальной метки. Два освещенных пикселя принадлежат одной области, если являются соседями. Рассмотрим, например, следующее изображение, в кото­ром освещенные пиксели сигнала обозначены точками, а неосвещенные — пробелами.



Глава 9. Модели взаимодействия процессов                                                                        335

В изображении есть три области. "Кривая" в правом нижнем углу не образует область, по­скольку ее точки соединены по диагоналям, а не горизонтальным или вертикальным линиям.16

Метки областей хранятся во второй матрице label [m, n]. Вначале каждая точка изобра­жения получает уникальную метку вроде линейной функции m* i+j от координат точки i и j. Окончательное значение элементов массива label [i, j ] должно быть равно максимальной из начальных меток в области, содержащей точку (i, j).

Естественный способ решения этой задачи — итерационный алгоритм. На каждой итера­ции просматриваются все точки и их соседи. Если текущий пиксель и его сосед имеют значе­ние 1, то меткой пикселя становится максимальная из меток его и соседа. Эти действия мож­но выполнять для всех пикселей параллельно, поскольку метки никогда не уменьшаются.

Алгоритм завершается, если в течение итерации не изменяется ни одна метка. Обычно области достаточно компактны, и алгоритм прекращает работу примерно через О(т) итера­ций. Однако в худшем случае потребуется О(т*п) итераций, поскольку область может "виться" по всему изображению.

В данной задаче пиксели независимы, поэтому можно использовать m*n параллельных задач. Это решение подходит для SIMD-машины с массовым параллелизмом, но для MIMD-машины такие маленькие задачи использовать неэффективно.


Предположим, что есть MIMD-машина с р процессорами, и m кратно р. Тогда было бы правильно решать задачу вы­деления областей, разделив изображение на р полос или блоков пикселей и назначив для ка­ждой полосы или блока отдельный рабочий процесс. Используем деление на полосы — оно проще программируется и требует меньшего числа сообщений, чем деление на блоки, по-. скольку у рабочих процессов меньше соседей. (На машинах, организованных как сетки или кубы, было бы эффективней использовать блоки точек, поскольку сеть связи в таких маши­нах поддерживает одновременные передачи сообщений.)

Каждый рабочий процесс вычисляет метки пикселей своей полосы. Для этого ему нужна собственная полоса изображения image и полоса матрицы меток label, а также значения граничных элементов полос, расположенных над и под его полосой. Поскольку области могут накрывать границы блоков, процесс должен взаимодействовать со своими соседями. Для этого на каждой итерации процесс обменивается метками пикселей на границах своей поло­сы с двумя соседями, а затем вычисляет новые метки.

В листинге 9.3, а показана схема рабочего процесса. После инициализации локальных пе­ременных рабочий процесс обменивается значениями на границе своей части матрицы im­age с соседями. Сначала он отправляет граничные значения соседу сверху и соседу снизу, за­тем получает значения от соседа снизу и от соседа сверху. Для обмена используются два мас­сива каналов first и second. Как показано на схеме, рабочие процессы 1 и Р представляют собой частные случаи, поскольку у них есть только по одному соседу.

В начале каждого повторения цикла while соседи-рабочие обмениваются граничными значениями своих частей массива label, используя описанную выше схему передачи сооб­щений. Затем они обновляют метки пикселей своей полосы. Код обновления мог бы обра­щаться к каждому пикселю один раз или выполняться циклически, пока изменяются метки в полосе. Последний способ приводит к меньшему числу сообщений для обмена метками между рабочими процессами, повышая производительность за счет уменьшения доли вычис­лений, необходимых для взаимодействия.



В этом приложении рабочий процесс не может сам определить, когда нужно завершить работу. Даже если на итерации не было локальных изменений, могли изменяться метки вдругой полосе, а соответствующие им пиксели могли принадлежать области, захватываю­щей несколько полос. Вычисления заканчиваются, только если не изменяются метки во всем изображении. (В действительности это происходит на одну итерацию раньше, но определить это сразу невозможно.)

16 Неявно предполагается, что область состоит из более, чем одного пикселя. — Прим. ред.



Для определения момента завершения программы используется управляющий процесс (листинг 9.3, б). (Его функции мог бы выполнять один из рабочих процессов, но для упроще­ния кода используется отдельный процесс.) В конце каждой итерации все рабочие процессы передают управляющему сообщения, указывающие, изменялись ли метки каждым из процес­сов. Управляющий процесс объединяет сообщения и отсылает рабочим ответ. Для этих взаи­модействий используются каналы result и answer [n].

^Листинг 9.3. б. Выделение областей: управляющий процесс

chan result(bool);  # для результатов от рабочих процессов

process Coordinator {

bool chg, change = true; while (change) { change = false;

# посмотреть, были ли изменения в полосах for [i = 1 to P] {

receive result(chg); change = change or chg; }

# разослать ответ всем рабочим процессам for [i = 1 to P]

send answer[i](change); }

2________________________________________________________

Глава 9. Модели взаимодействия процессов                                                                      337

Для проверки завершения работы с помощью управляющего процесса на одной итерации нужно обменяться 2 *Р сообщениями. Если бы ответ управляющего процесса мог рассылать­ся сразу всем рабочим, то было бы достаточно р+1 сообщений. Однако в обоих случаях время работы управляющего процесса составляет О(Р), поскольку он получает сообщения с резуль­татами по одному. Используя дерево управляющих процессов, общее время их работы можно снизить до 0(log2P).


Еще лучше, если доступна операция редукции (сведения) для глобаль­ного сбора сообщений, например, операция MPi_AllReduce из библиотеки MPI. В резуль­тате упростится код программы и, возможно, повысится производительность, в зависимости от того, как реализована библиотека MPI на данной машине.

9.2.2. Клеточный автомат: игра "Жизнь"

Многие биологические и физические системы можно промоделировать в виде набора объектов, которые с течением времени циклически взаимодействуют и развиваются. Некото­рые системы, особенно простые, можно моделировать с помощью клеточных автоматов. (Более сложная система— гравитационное взаимодействие— рассматривается в главе 11.) Основная идея — разделить пространство физической или биологической задачи на отдель­ные клетки. Каждая клетка — это конечный автомат. После инициализации все клетки сна­чала совершают один переход в новое состояние, затем второй переход и т.д. Результат каж­дого перехода зависит от текущего состояния клетки и ее соседей.

Здесь клеточный автомат использован для моделирования так называемой игры "Жизнь". Дано двухмерное поле клеток. Каждая клетка либо содержит организм (жива), либо пуста (мертва). Бэтой задаче каждая клетка имеет восемь соседей, которые расположены сверху, снизу, слева, справа и по четырем диагоналям от нее. У клеток в углах по три соседа, а на границах — по пять.

Игра "Жизнь" происходит следующим образом. Сначала поле инициализируется. Затем каждая клетка проверяет состояние свое и своих соседей и изменяет свое состояние в соот­ветствии со следующими правилами.

•    Живая клетка, возле которой меньше двух живых клеток, умирает от одиночества.

•    Живая клетка, возле которой есть две или три живые клетки, выживает еще на одно поколение.

•    Живая клетка, возле которой находится больше трех живых клеток, умирает от пе­ренаселения.

•    Мертвая клетка, рядом с которой есть ровно три живых соседа, оживает.

Этот процесс повторяется некоторое число шагов (поколений).



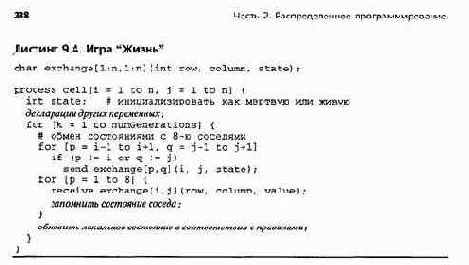
Листинг 9. 4 содержит схему программы для имитации игры "Жизнь". Процессы взаимо­действуют с помощью парадигмы пульсации. На каждой итерации клетка посылает сообще­ния каждому из соседей и получает сообщения от них, после чего обновляет свое состояние в соответствии с приведенными правилами. Как обычно при использовании алгоритма пуль­сации, для процессов не нужна жесткая пошаговая синхронизация, но соседи никогда не опережают друг друга более, чем на одну итерацию.

Для простоты каждая клетка запрограммирована как процесс, хотя поле можно разделить на полосы или блоки клеток. Также не учтены особые случаи угловых и граничных клеток. Каждый процесс eel I [ i, j ] получает сообщения из элемента exchange [ i, j ] матрицы ка­налов связи, а отсылает сообщения в соседние элементы матрицы exchange. (Напомним, что каналы буферизуются, а операция send — неблокирующая.) Читателю было бы полезно реализовать эту программу с отображением состояния клеток в графической форме.

было бы объявить как first [1-.P-1] и second [2 :Р]. — Прим. ред.




Содержание раздела

---

---