Алгоритмы передачи маркера

В этом разделе описывается передача маркера — еще одна модель взаимодействия про­цессов. Маркер — это особый тип сообщений, который можно использовать для передачи разрешения или сбора информации о глобальном состоянии. Использование маркера для передачи разрешения иллюстрируется простым распределенным решением задачи крити­ческой секции. Сбор информации о состоянии демонстрируется в процессе разработки двух алгоритмов, позволяющих определить, завершились ли распределенные вычисления. Еще один пример приводится в следующем разделе (см. также историческую справку и уп­ражнения).

9.6.1. Распределенное взаимное исключение

Задача о критической секции (КС) возникла в программах с разделяемыми переменными. Однако она встречается и в распределенных программах, если какой-нибудь разделяемый ре­сурс используется в них с исключительным доступом. Это может быть, например, линия свя­зи со спутником. Кроме того, задача КС обычно является частью большей задачи, такой как обеспечение согласованности распределенного файла или системы баз данных.

Первый способ решения задачи КС — использовать активный монитор, разрешающий доступ к КС. Для многих задач вроде реализации блокировки файлов это самый простой и эффективный метод. Второй способ решения этой задачи — использовать распределенные семафоры, реализованные так, как описано в предыдущем разделе. Этот способ приводит к децентрализованному решению, в котором все процессы одинаковы, но для каждой опера­ции с семафором необходим обмен большим количеством сообщений, поскольку операция broadcast должна быть подтверждена.

Здесь задача решается третьим способом — с помощью кольца передачи маркера (token nng). Это децентрализированное и справедливое решение, как и решение с использованием распределенных семафоров, но оно требует обмена намного меньшим количеством сообще­ний. Кроме того, базовый метод можно обобщить для решения других задач синхронизации.

Пусть User [ 1: п ] — это набор прикладных процессов, содержащих критические и некри­тические секции.
Как всегда, нужно разработать протоколы входа и выхода, которые выпол­няются перед КС и после нее. Протоколы должны обеспечивать взаимное исключение, от­сутствие блокировок и ненужных задержек, а также возможность входа (справедливость).

Поскольку у пользовательских процессов есть своя работа, нам не нужно, чтобы они за­нимались передачей маркера. Используем набор дополнительных процессов Helper [ 1: п], по одному для каждого пользовательского процесса. Вспомогательные процессы образуют кольцо (рис. 9.3). Маркер циркулирует от процесса Helper [ 1 ] к процессу Helper [2 ] и так далее до процесса Helper [n], который передает его процессу Helper [1]. Получив маркер,

354                                                                        Часть 2. Распределенное программирование

Helper [i] проверяет, не собирается ли входить в КС его клиент User[i]. Если нет, Helper [ i ] передает маркер. Иначе Helper [ i ] сообщает процессу User [ i ], что он может войти в КС, и ждет, пока процесс User [ i ] не выйдет из нее. После этого Helper [ i ] пере­дает маркер. Таким образом, вспомогательные процессы работают совместно, чтобы обеспе­чить постоянное выполнение следующего предиката.

Решение в листинге 9.12 является справедливым (при условии, что процессы когда-нибудь выходят из критических секций). Причина в том, что маркер циркулирует непре­рывно, и как только он оказывается у процесса Helper[i], процесс Userfi] получает разрешение войти в КС (если хочет). Фактически то же самое происходит и в физической сети с передачей маркера. Однако при программной передаче маркера, вероятно, лучше добавить некоторую задержку во вспомогательных процессах, чтобы он двигался по кольцу медленней. (В разделе 9.7 представлен еще один алгоритм исключения на основе передачи маркера. Там маркеры не циркулируют непрерывно.)

Данный алгоритм предполагает отсутствие сбоев и потерь маркера. Поскольку управление распределено, алгоритм можно изменить, чтобы он стал устойчивым к сбоям.




Алгоритмы восстановления потерянного маркера и использования двух маркеров, циркулирующих в противоположных направлениях, описаны в исторической справке.

9.6.2. Как определить окончание работы в кольце

Окончание работы последовательной программы обнаружить легко. Так же легко опреде­лить, что параллельная программа завершилась на одном процессоре — каждый процесс за­вершен или заблокирован и нет ожидающих операций ввода-вывода. Но не просто обнару­жить, что закончилась распределенная программа, поскольку ее глобальное состояние не видно ни одному процессору. Кроме того, даже если все процессоры бездействуют, могут су­ществовать сообщения, передаваемые между ними.

Существует несколько способов обнаружить завершение распределенных вычислений. В этом разделе разрабатывается алгоритм, основанный на передаче маркера при условии, что все взаимодействие между процессами происходит по кольцу. В следующем разделе этот ал­горитм обобщается для полного графа связей. Другие подходы описаны в исторической справке и упражнениях.

Пусть в распределенных вычислениях есть процессы (задачи) Т[1.-п] и массив каналов взаимодействия ch [1 :п]. Пока предположим, что процессы образуют кольцо, по которому проходит их взаимодействие. Процесс T[i] получает сообщения только из своего канала ch[i] и передает их только в следующий канал ch[i%n+l]. Таким образом, Т[1] передает сообщения только Т [ 2 ], Т [ 2 ] — только Т [ 3 ] и так далее до Т [n ], передающего сообщения Т[1]. Как обычно, предполагается, что сообщения от каждого процесса его сосед по кольцу получает в порядке их передачи.

В любой момент времени процесс может быть активным или простаивать (бездействовать). Вначале активны все процессы. Процесс бездействует, если он завершен или приостановлен оператором получения сообщения. (Если процесс временно приостанав­ливается, ожидая окончания операции ввода-вывода, он считается активным, поскольку он еще не завершен и через некоторое время снова будет запущен.) Получив сообщение, бездей­ствующий процесс становится активным.


Таким образом, распределенные вычисления за­кончены, если выполняются следующие два условия:

DTERM:  все процессы бездействуют л нет передаваемых сообщений

Сообщение передается (находится в пути), если оно уже отправлено, но еще не доставлено вканал назначения. Второе условие обязательно, поскольку доставленное сообщение может запустить приостановленный процесс.

356                                                                            Часть 2. Распределенное программирование

Наша задача — перенести алгоритм определения окончания работы на любые распределен­ные вычисления, основываясь только на предположении о том, что процессы в вычислении взаимодействуют по кольцу. Окончание — это свойство глобального состояния, объединяющего состояния отдельных процессов и содержание каналов передачи сообщений. Таким образом, чтобы определить момент окончания вычислений, процессы должны взаимодействовать.

Пусть один маркер передается по кольцу в специальных сообщениях, не являющихся ча­стью вычислений. Процесс, удерживающий маркер, передает его дальше и становится без­действующим. (Если процесс закончил свои вычисления, он бездействует, но продолжает участвовать в алгоритме обнаружения завершения работы.)

Процессы передают маркер, используя то же кольцо каналов связи, что и в самих вычис­лениях. Получая маркер, процесс знает, что отправитель в момент передачи маркера бездей­ствовал. Кроме того, получая маркер, процесс бездействует, поскольку был задержан получе­нием сообщения из канала, и не станет активным до тех пор, пока не получит обычное сооб­щение, являющееся частью распределенных вычислений. Таким образом, получая маркер, процесс передает его соседу и ждет получения еще одного сообщения из своего канала.

Вопрос в том, как определить, что вычисления завершились. Когда маркер совершает полный круг по кольцу взаимодействия, нам точно известно, что в этот момент все процессы бездействуют. Но как владелец маркера может определить, что все остальные процессы по-прежнему бездействуют и ни одно сообщение не находится в пути к получателю?



Допустим, что вначале маркер находится у процесса т [ 1 ]. Когда Т [ 1 ] становится без­действующим, он инициирует алгоритм обнаружения окончания работы, передавая маркер процессу Т [2]. Возвращение маркера к Т[1] означает, что вычисления закончены, если Т [ 1 ] был непрерывно бездействующим с момента передачи им маркера процессу Т [ 2 ]. Дело в том, что маркер проходит по тому же кольцу, по которому идут обычные сообщения, а все сообщения доставляются в порядке их отправки. Таким образом, если маркер возвра­щается к т [ 1 ], значит, ни одного обычного сообщения уже не может быть нигде в очереди или в пути. По сути, маркер "очищает" каналы, проталкивая перед собой все обычные со­общения.

Уточним алгоритм. Во-первых, с каждым процессом свяжем цвет: синий (холодный), если процесс бездействует, и красный (горячий), если он активен. Вначале все процессы активны, поэтому окрашены красным. Получая маркер, процесс бездействует, поэтому становится си­ним, передает маркер дальше и ждет следующее сообщение. Получив позже обычное сооб­щение, процесс станет красным. Таким образом, процесс, окрашенный в синий цвет, передал маркер дальше и остался бездействующим.

Во-вторых, с маркером свяжем значение, которое показывает количество пустых каналов, если Т[1] остается бездействующим. Пусть это значение хранится в переменной token. Становясь бездействующим, Т [ 1 ] окрашивается в синий цвет, присваивает token значение О и передает маркер процессу Т [ 2 ]. Получая маркер, Т [ 2 ] бездействует (при этом канал сп[2] может быть пустым). Поэтому Т [2] становится синим, увеличивает значение token до 1 и передает маркер процессу Т [ 3 ]. Все процессы Т [ i ] по очереди становятся синими и увеличивают token перед тем, как передать дальше.

Описанные правила передачи маркера перечислены в листинге 9.13. Их выполнение га­рантирует, что условие RING является глобальным инвариантом. Инвариантность RING следует из того, что, если процесс Т [1] окрашен в синий цвет, значит, с момента передачи маркера никаких обычных сообщений он не передавал, и, следовательно, ни в одном из каналов, пройденных маркером, нет обычных сообщений.


Кроме того, все соответствую­щие процессы остались бездействующими с тех пор, как получили маркер. Таким образом, если Т[1] остался синим, снова получив маркер, то все остальные процессы тоже окраше­ны в синий цвет, а каналы — пусты. Следовательно, т [ 1 ] может объявить, что вычисления закончены.



9.6.3. Определение окончания работы в графе

В предыдущем разделе предполагалось, что все взаимодействия происходят по кольцу. В общем случае структура взаимодействия распределенной программы образует произволь­ный ориентированный граф. Узлы графа представляют процессы в вычислениях, а дуги — пу­ти взаимодействия. Два процесса связаны дугой, если первый из них передает данные в ка­нал, из которого их считывает второй.

Предположим, что граф связей является полным, т.е. между любыми двумя процессами есть одна дуга. Как и ранее, есть п процессов Т [ 1: n ] и каналов ch [ 1: n ], и каждый Т [ i ] по­лучает данные из собственного канала ch [ i ]. Однако теперь каждый процесс может посы­лать сообщения только в канал ch [ i ].

Учитывая вышесказанное, расширим предыдущий алгоритм определения окончания ра­боты. Полученный в результате алгоритм можно использовать в любой сети, имеющей пря­мые линии взаимодействия между любыми двумя процессорами. Его легко распространить на произвольные графы взаимодействия и многоканальные связи (см. упражнения).

Определить окончание работы в полном графе сложнее, чем в кольце, поскольку сообще­ния могут идти по любой дуге Рассмотрим, например, полный граф из трех процессов (рис. 9.4). Пусть процессы передают маркер только от Т [ 1 ] к Т [ 2 ], затем к Т [3 ] и обратно к т [ 1 ]. Допустим, процесс т [ 1 ] получает маркер и становится бездействующим; следова­тельно, он передает маркер процессу Т [2}. Становясь бездействующим, Т [2 ] передает мар­кер Т [ 3 ]. Но перед получением маркера Т [ 3 ] может передать процессу Т [ 2 ] обычное сооб­щение. Таким образом, когда маркер возвращается к Т [ 1 ], нельзя сделать вывод о том, что вычисления завершены, даже если т [ 1 ] оставался непрерывно бездействующим.



Основным в кольцевом алгоритме (см. листинг 9.13) является то, что все взаимодействия проходят по кольцу, поэтому маркер "проталкивает" обычные сообщения, проходя все дуги кольца. Этот алгоритм можно обобщить для полного графа, обеспечив проход маркера по ка­ждой дуге (маркер должен многократно посетить каждый процесс). Если каждый процесс ос­тается непрерывно бездействующим с момента предыдущего получения маркера, то можно прийти к выводу, что вычисления завершены.

Как и раньше, процессы окрашиваются в красный или синий цвет (вначале — в красный). Получая обычное сообщение, процесс становится красным, а получая маркер, — блокируется в ожидании следующего сообщения из своего входного канала. Поэтому процесс окрашива­ется в синий цвет (если он еще не был синим) и передает маркер. (Как и раньше, заканчивая свои обычные вычисления, процесс продолжает обрабатывать сообщения с маркером.)

358                                                                            Часть 2 Распределенное программирование

Любой полный граф содержит цикл, в который входят все его дуги (некоторые узлы могут включаться несколько раз). Пусть С — цикл графа взаимодействия, а nс — его длина. Каждый процесс отслеживает порядок, в котором исходящие из него дуги встречаются в цикле с. По­лучив маркер по одной дуге цикла с, процесс передает его по следующей. Это гарантирует, что маркер пройдет по каждой дуге графа взаимодействия.



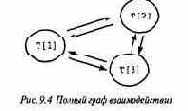
Как и раньше, маркер имеет значение, говорящее о количестве пройденных бездействующих процессов и, следовательно, каналов, которые могут быть пустыми. Но из приведенного выше примера видно, что в полном графе бездействующий процесс снова может стать активным, даже если бездействующим остается процесс Т [ 1 ]. Таким образом, чтобы делать вывод об окончании вычислений, нужен другой набор правил передачи маркера и другой глобальный инвариант.

Маркер начинает движение с любого процесса и имеет начальное значение 0. Когда этот процесс впервые становится бездействующим, он окрашивается в синий цвет и передает мар­кер по первому ребру цикла С.


Получив маркер, процесс совершает действия, представлен­ные в листинге 9.14. Если при получении маркера процесс окрашен в красный цвет (с момен­та последнего получения маркера он был активным), он становится синим и присваивает маркеру token значение О перед тем, как передать его по следующему ребру цикла С. Таким образом, алгоритм обнаружения окончания программы перезапускается. Но если при полу­чении маркера процесс окрашен в синий цвет, т.е. с момента последнего получения маркера непрерывно бездействовал, то перед передачей маркера процесс увеличивает его значение.



Глава 9 Модели взаимодействия процессов                                                                        359

числения закончены. В этот момент известно, что последние пс каналов, пройденные марке­ром, были пустыми. Поскольку бездействующий процесс только передает маркер, а значение маркера увеличивает, только если бездействовал с момента прошлого получения маркера, можно наверняка сказать, что все каналы пусты и все процессы бездействуют. В действитель­ности все вычисления завершились уже к тому моменту, когда маркер начал свой последний проход по графу. Но ни один процесс не может это установить до тех пор, пока маркер не сделает еще один полный цикл по графу, чтобы убедиться в том, что все процессы остались бездействующими и все каналы — пустыми. Таким образом, после завершения всех вычисле­ний маркер должен пройти по циклу как минимум дважды: на первом проходе процессы ста­новятся синими, а на втором — проверяется, не поменяли ли они цвет.


Содержание раздела

---

---