Алгоритмы, параллельные по данным

В алгоритмах, параллельных по данным, несколько процессов выполняют один и тот же код и работают с разными частями разделяемых данных. Для синхронизации выполнения от­дельных фаз процессов используются барьеры. Этот тип алгоритмов теснее всего связан с синхронными мультипроцессорами, или SIMD-машинами, т.е. машинами с одним потоком инструкций и многими потоками данных (single instruction, multiple data— SIMD). В SIMD-машинах аппаратно поддерживаются мелкомодульные вычисления и барьерная синхрониза­ция. Однако алгоритмы, параллельные по данным, полезны и в асинхронных мультипроцес­сорных машинах при условии, что затраты на барьерную синхронизацию с лихвой компенси­руются высокой степенью параллелизма процессов.

В данном разделе разработаны решения, параллельные по данным, для трех задач: час­тичное суммирование массива, поиск конца связанного списка и итерационный метод Якоби для решения дифференциальных уравнений в частных производных. Они иллюстрируют ос­новные методы, используемые в алгоритмах, параллельных по данным, и барьерную синхро­низацию. В конце раздела описаны многопроцессорные SIMD-машины и показано, как они помогают избежать взаимного влияния процессов и, следовательно, избавиться от необходи­мости программирования барьеров. Эффективной реализации алгоритмов, параллельных по данным, на машинах с разделяемой и распределенной памятью посвящена глава 11.

3.5.1. Параллельные префиксные вычисления

Часто бывает нужно применить некоторую операцию ко всем элементам массива. Напри­мер, чтобы вычислить среднее значение числового массива а [n], нужно сначала сложить все элементы массива, а затем разделить сумму на п. Иногда нужно получить средние значения для всех префиксов а [ 0 : i] массива. Для этого нужно вычислить суммы всех префиксов. Та­кой тип вычислений очень часто встречается, поэтому, например, в языке APL есть даже спе­циальные операторы редукции ("сворачивания") reduce и просмотра scan. SIMD-машины с массовым параллелизмом вроде Connection Machine обеспечивают аппаратную реализацию операторов редукции для упаковки значений в сообщения.

В данном разделе показано, как параллельно вычисляются суммы всех префиксов масси­ва. Эта операция называется параллельным префиксным вычислением. Базовый алгоритм может быть использован с любым ассоциативным бинарным оператором (сложение, умножение, логические операторы, вычисление максимума и другие). Поэтому параллельные префикс­ные вычисления используются во многих приложениях, включая обработку изображений, матричные вычисления и анализ регулярных языков (см. упражнения в конце главы).

Пусть дан массив а [n] и нужно вычислить sum[n], где sum[ i] означает сумму первых 1 элементов массива а. Очевидный способ последовательного решения этой задачи — пройти по элементам двух массивов.

sum [ 0]   = а [ 0 ] ; for   [i =  1 to n-1]

sum[i]   =  sum[i-l]   + a[i];

Глава 3. Блокировки и барьеры                                                                                                   111

На каждой итерации значение а [ i ] прибавляется к уже вычисленной сумме предыдущих i-l элементов.

Теперь посмотрим, как этот алгоритм можно распараллелить. Если нужно просто найти сумму всех элементов, можно выполнить следующее. Сначала параллельно сложить пары элементов массива, например, складывать а [ 0 ] и а [ 1 ] синхронно с другими парами. После этого (тоже параллельно) объединить результаты первого шага, например, сложить сумму а [ 0 ] и а [ 1 ] с суммой а [ 2 ] и а [ 3 ] параллельно с вычислением других частичных сумм. Ес­ли этот процесс продолжить, то на каждом шаге количество просуммированных элементов будет удваиваться. Сумма всех элементов массива будет вычислена за flog2n] шагов. Это луч­шее, что можно сделать, если элементы обрабатываются парами.

Для параллельного вычисления сумм всех префиксов можно адаптировать описанный ме­тод удвоения числа обработанных элементов. Сначала присвоим всем элементам sum [ i ] значения a [i]. Затем параллельно сложим значения sum[i-l] и sum[i] для всех i >= 1, т.е. сложим все элементы, которые находятся на расстоянии 1.


Теперь удвоим расстояние и сложим элементы sum [i-2] с sum [ i ], на этот раз для всех i >= 2. Если продолжать уд­ваивать расстояние, то после [log2n] шагов будут вычислены все частичные суммы. Следую­щая таблица иллюстрирует шаги алгоритма для массива из шести элементов.





В листинге 3.14 представлена реализация этого алгоритма. Каждый процесс сначала ини­циализирует один элемент массива sum, а затем циклически вычисляет частичные суммы. Про­цедура barrier (i), вызываемая в программе, реализует точку барьерной синхронизации, ар­гумент i — идентификатор вызывающего процедуру процесса. Выход из процедуры происходит, когда все n процессов выполнят команду barrier. В теле процедуры может быть использован один из алгоритмов, описанных в предыдущем разделе. (Для этой задачи барьеры можно опти­мизировать, поскольку на каждом шаге синхронизируются только два процесса.)



112                                               Часть 1. Программирование с разделяемыми переменными

sum[i] должен сохранить копию его старого значения. Инвариант цикла SUM определяет, какая часть префикса массива а просуммирована на каждой итерации.

Как уже было отмечено, этот алгоритм можно изменить для использования с любым ассо­циативным бинарным оператором. Для этого достаточно поменять оператор, преобразующий элементы массива sum. Выражение для комбинирования результатов записано в виде old [ i-d] + sum[i], поэтому бинарный оператор не обязан быть коммутативным. Программу 3.14 можно адаптировать и для числа процессов меньше n; тогда каждый процесс будет отвечать за объединение частичных сумм полосы массива.

3.5.2. Операции со связанными списками

При работе со связанными структурами данных типа деревьев для поиска и вставки элементов за время, пропорциональное логарифму, часто используются сбалансированные бинарные дере­вья. Однако при использовании алгоритмов, параллельных по данным, многие операции даже с линейными списками можно реализовать за логарифмическое время.


Покажем, как найти конец последовательно связанного списка. Этот же алгоритм можно использовать и для других операций над последовательно связанными списками, например, вычисления всех частичных сумм значе­ний, вставки элемента в список приоритетов или поэлементного сравнения двух списков.

Предположим, что есть связанный список, содержащий не более n элементов. Связи хранятся в массиве link [n], а данные — в массиве data [n]. На начало списка указывает еще одна пере­менная, head. Если элемент i является частью списка, то или head == i, или link[ j ] == i для некоторого j от 0 до п-1. Поле link последнего элемента списка является указателем "в ни­куда" (пустым), что обозначается null. Предположим, что поля link элементов вне списка также пусты, а список уже инициализирован. Ниже приводится пример такого списка.



 Задача состоит в том, чтобы найти конец списка. Стандартный последовательный алго­ритм начинает работу с начала списка head и следует по ссылкам, пока не найдет пустой ука­затель. Последний из просмотренных элементов и есть конец списка. Время работы этого алгоритма пропорционально длине списка. Однако поиск конца списка можно выполнить за время, пропорциональное логарифму его длины, если использовать алгоритм, параллельный по данным, и метод удвоения из предыдущего раздела.

Каждому элементу списка назначается процесс Find. Пусть end[n] — разделяемый мас­сив целых чисел. Если элемент i является частью списка, то задача процесса F ind [ i ] — при­своить переменной end [ i] значение, равное индексу последнего элемента списка, в против­ном случае процесс Find[i] должен присвоить end[i] значение null. Чтобы не рассмат­ривать частные случаи, допустим, что список содержит хотя бы два элемента.

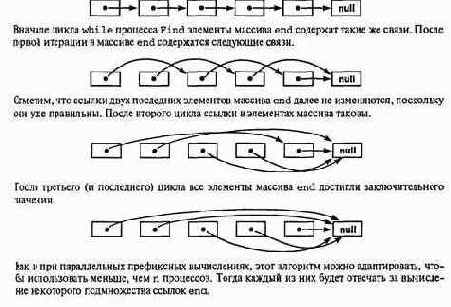
В начале работы каждый процесс присваивает элементу end [ i ] значение 1 ink [ i ], т.е. ин­декс следующего элемента списка (если он есть). Таким образом, массив end в начале работы воспроизводит схему связей списка. Затем процессы выполняют ряд этапов.


На каждом этапе процесс рассматривает элемент с индексом end [ end [i]]. Если элементы end [end [i]] nend[i] — не пустые указатели, то процесс присваивает элементу end[i] значение end [end [i] ]. Таким образом, после первого цикла переменная end[i] будет указывать на элемент списка, находящийся на расстоянии в две связи от начального (если такой есть). После двух циклов значение end [ i ] будет указывать на элемент списка, удаленный на четыре связи (опять-таки, если он существует). После [log2n] циклов каждый процесс найдет конец списка.



В листинге 3.15 представлена реализация этого алгоритма. Поскольку метод программи­рования тот же, что и для параллельных префиксных вычислений, структура алгоритма такая же, как в листинге 3.14. barrier (i) — это вызов процедуры, реализующей барьерную син­хронизацию процесса 1. Инвариант цикла FIND определяет, на что указывает элемент масси­ва end [ i ] до и после каждой итерации. Если конец списка находится от элемента i на рас­стоянии не более 2Л~1

связей, то в дальнейших итерациях значение end [ i ] не изменится.

Для иллюстрации работы алгоритма рассмотрим следующий список из шести элементов.



114                                              Часть 1 Программирование с разделяемыми переменными

3.5.3. Сеточные вычисления: итерация Якоби

Многие задачи обработки изображений или научного моделирования решаются с помощью так называемых сеточных вычислений. Они основаны на использовании матрицы точек (сетки), на­ложенной на область пространства. В задаче обработки изображений матрица инициализируется значениями пикселей (точек), а целью является поиск чего-то вроде множества соседних пикселей с одинаковой интенсивностью. В научном моделировании часто используются приближенные ре­шения дифференциальных уравнений в частных производных; в этом случае граничные элементы матрицы инициализируются краевыми условиями, а цель состоит в приближенном вычислении значений в каждой внутренней точке. (Это соответствует поиску устойчивого решения уравнения.) В любом случае, сеточные вычисления имеют следующую общую схему.



инициализировать матрицу; whilе   (еще не завершено)   {

для каждой точки вычислить новое значение;

проверить условие завершения; }

Обычно на каждой итераций новые значения точек вычисляются параллельно.

В качестве конкретного примера приведем простое решение уравнения Лапласа для двух­мерного случая: Д2 = 0. (Это дифференциальное уравнение в частных производных; подробно­сти— в разделе 11.1.) Пусть grid[n+l,n+l] — матрица точек. Границы массива grid (левый и правый столбцы, верхняя и нижняя строки) представляют края двухмерной области. Сетке, наложенной на область, соответствуют nхn внутренних элементов массива grid. Задача — вы­числить устойчивые значения внутренних точек. Для уравнения Лапласа можно использовать метод конечных разностей типа итераций Якоби. На каждой итерации новое значение каждой внутренней точки вычисляется как среднее значение четырех ее ближайших соседей.

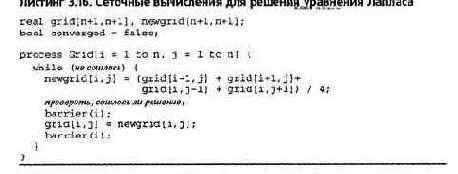
В листинге 3.16 представлены сеточные вычисления для решения уравнения Лапласа с помощью итераций Якоби. Для синхронизации шагов вычислений вновь применяются барьеры. Каждая итерация состоит из двух основных шагов: обновление значений newgrid с проверкой на сходимость и перемещение содержимого массива newgrid в массив grid. Для того чтобы новые сеточные значения зависели только от старых, используются две мат­рицы. Вычисления можно закончить либо после фиксированного числа итераций, либо при достижении заданной точности, когда новые значения newgrid будут отличаться от значе­ний grid не более, чем на EPSILON. Разности можно вычислять параллельно, но с после­дующим объединением результатов. Это можно сделать с помощью параллельных префикс­ных вычислений; решение оставляется читателю (см. упражнения в конце главы).



Глава 3. Блокировки и барьеры                                                                                                15

Алгоритм в листинге 3.16 правилен, но в некоторых отношениях слишком упрощен. Во-"яервых, массив newgrid копируется в массив grid на каждой итерации.


Было бы намного эффективнее "развернуть" цикл, чтобы на каждой итерации сначала обновлялись значения, переходящие из grid в newgrid, а затем — из newgrid в grid. Во-вторых, лучше использо­вать алгоритм последовательной сверхрелаксации, сходящийся быстрее. В-третьих, програм­ма в листинге 3.16 является слишком мелкомодульной для асинхронных мультипроцессоров. Поэтому гораздо лучше разделить сетку на блоки и каждому блоку назначить один процесс (и процессор). Все эти нюансы подробно рассмотрены в главе 11, где показано, как эффек­тивно выполнять сеточные вычисления и на мультипроцессорах с разделяемой памятью, и на машинах с распределенной памятью.

3.5.4. Синхронные мультипроцессоры

В асинхронном мультипроцессоре все процессоры выполняют разные процессы с потен­циально разными скоростями. Такие мультипроцессоры называются MIMD-машинами (multiple instruction — multiple data, много команд — много данных), поскольку имеют не­сколько потоков команд и данных, т.е. состоят из нескольких независимых процессоров. Обычно предполагается именно такая модель выполнения.

MIMD-машины являются наиболее гибкими мультипроцессорами, поэтому используют­ся чаще других. Однако в последнее время стали доступными и синхронные мультипроцессо­ры (SIMD-машины), например, Connection Machine (начало 1990-х) или машины Maspar (середина-конец 1990-х). В SIMD-машине несколько потоков данных, но только один поток инструкций. Все процессоры синхронно выполняют одну и ту же последовательность команд. Это делает SIMD-машины особенно подходящими для алгоритмов, параллельных по дан­ным. Например, алгоритм 3.14 вычисления всех частичных сумм массива для SIMD-машины упрощается следующим образом.



Программные барьеры не нужны, поскольку все процессы одновременно выполняют одни и те же команды, следовательно, каждая команда и обращение к памяти сопровождаются не­явным барьером. Кроме того, для хранения старых значений не нужны дополнительные пе­ременные.


При присваивании значения элементу sum [ i ] каждый процесс(ор) извлекает из массива sum старые значения элементов перед тем, как присваивать новые. По этой причине параллельные инструкции присваивания на SIMD-машине становятся неделимыми, в ре­зультате чего исключаются некоторые источники взаимного влияния процессов.

Создать SIMD-машину с большим числом процессоров технологически намного проще, чем построить MIMD-машину с массовым параллелизмом. Это делает SIMD-машины привлека­тельными для решения больших задач, в которых можно использовать алгоритмы, параллель­ные по данным. С другой стороны, SIMD-машины являются специализированными, т.е. в лю­бой момент времени вся машина выполняет одну программу. (Это основная причина, по кото­рой интерес к SIMD-машинам невелик.) Кроме того, программисту нелегко все время загружать каждый процессор полезной работой. В приведенном выше алгоритме, например, все меньше и меньше процессоров на каждой итерации обновляют элементы sum [ i ], но все они

116                                               Часть 1 Программирование с разделяемыми переменными

должны вычислять значение условия в операторе if. Если условие не выполняется, то процесс приостанавливается, пока все остальные не обновят значения элементов массива sum. Таким образом, время выполнения оператора if — это общее время выполнения всех ветвей, даже если какая-то из них не затрагивается. Например, время выполнения оператора if /then/else на каж­дом процессоре — это сумма времени вычисления условия, выполнения then- или else-ветви.

3.6. Параллельные вычисления с портфелем задач

Как указано в предыдущем разделе, многие итерационные задачи могут быть решены с помощью программирования, параллельного по данным. Решение рекурсивных задач, ос­нованное на принципе "разделяй и властвуй", можно распараллелить, выполняя рекурсив­ные вызовы параллельно, а не последовательно, как было показано в разделе 1.5.

В данном разделе представлен еще один способ реализации параллельных вычислений, в котором используется так называемый портфель задач. Задача является независимой еди­ницей работы.


Задачи помещаются в портфель, разделяемый несколькими рабочими процес­сами. Каждый рабочий процесс выполняет следующий основной код. while   (true)   {

получить задачу из портфеля ; if   (задач болыиенет)

break;        #  выход их цикла while

выполнить задачу, возможно, порождая новые задачи; }

Этот подход можно использовать для реализации рекурсивного параллелизма; тогда задачи будут представлены рекурсивными вызовами. Его также можно использовать для решения итеративных проблем с фиксированным числом независимых задач.

Парадигма портфеля задач имеет несколько полезных свойств. Во-первых, она весьма проста в использовании. Достаточно определить представление задачи, реализовать портфель, запрограм­мировать выполнение задачи и выяснить, как распознается завершение работы алгоритма. Во-вторых, программы, использующие портфель задач, являются масштабируемыми в том смысле, что их можно использовать с любым числом процессоров; для этого достаточно просто изменить коли­чество рабочих процессов. (Однако производительность программы при этом может и не изме­няться.) И, наконец, эта парадигма упрощает реализацию балансировки нагрузки. Если длитель­ности выполнения задач различны, то, вероятно, некоторые из задач будут выполняться дольше других. Но пока задач больше, чем рабочих процессов (в два—три раза), общие объемы вычисле­ний, осуществляемых рабочими процессорами, будут примерно одинаковыми.

Ниже показано, как с помощью портфеля задач реализуется умножение матриц и адап­тивная квадратура. При умножении матриц используется фиксированное число задач. В адаптивной квадратуре задачи создаются динамически. В обоих примерах для защиты дос­тупа к портфелю задач применяются критические секции, а для обнаружения окончания — барьероподобная синхронизация.

3.6.1. Умножение матриц

Вновь рассмотрим задачу умножения матриц а и Ь размером n x п. Это требует вычис­ления п2 промежуточных произведений, по одному на каждую комбинацию из строки а и столбца Ь.


Каждое промежуточное умножение — это независимое вычисление, которое можно выполнить параллельно. Предположим, однако, что программа будет выполняться на машине с числом процессоров PR. Тогда желательно использовать PR рабочих процессов, по одному на каждый процессор. Чтобы сбалансировать вычислительную загрузку, процессы

Глава 3. Блокировки и барьеры                                                                                    117r

должны вычислять примерно поровну промежуточных произведений. В разделе 1.4 каждому рабочему процессу часть вычислений назначалась статически. В данном случае воспользуем­ся портфелем задач, и каждый рабочий процесс будет захватывать задачу при необходимости. Если число PR намного меньше, чем n, то подходящий для задания объем работы — одна или несколько строк результирующей матрицы с. (Это ведет к разумной локализации матриц а и с с учетом того, что данные в них хранятся по строкам.) Для простоты используем оди­ночные строки. В начальном состоянии портфель содержит n задач, по одной на строку. За­дачи могут быть расположены в любом порядке, поэтому портфель можно представить про­стым перечислением строк.

int  nextRow =   0;

Рабочий процесс получает задачу из портфеля, выполняя неделимое действие

{ row = nextRow;   nextRow++;   )

Здесь row — локальная переменная. Портфель пуст, когда значение row не меньше п. Неде­лимое действие в указанной строке программы — это еще один пример вытягивания билета. Его можно реализовать с помощью инструкции "извлечь и сложить", если она доступна, или блокировок для защиты критической секции.

В листинге 3.17 представлена схема программы. Предполагается, что матрицы инициализи­рованы. Рабочие процессы вычисляют внутренние произведения обычным способом. Про­грамма завершается, когда все рабочие процессы выйдут из цикла while. Для определения этого момента можно воспользоваться разделяемым счетчиком done с нулевым начальным зна­чением. Перед тем как рабочий процесс выполнит оператор break, он должен увеличить значе­ние счетчика в неделимом действии.


Если нужно, чтобы последний рабочий процесс выводил результаты, в конец кода каждого рабочего процесса можно добавить следующие строки. if (done == n)

напечатать матрицу с;



118                                               Часть 1 Программирование с разделяемыми переменными

ной точностью равна большей, то приближение считается достаточно хорошим. Если нет, большая задача делится на две подзадачи, и процесс повторяется.

Парадигму портфеля задач можно использовать для реализации адаптивной квадратуры. Задача представляет собой отрезок для проверки; он определяется концами интервала, зна­чениями функции в этих точках и приближением площади для этого интервала. Сначала есть одна задача — для всего отрезка от а до Ь.

Рабочий процесс циклически получает задачу из портфеля и выполняет ее. В отличие от программы умножения матриц, в данном случае портфель задач может быть (временно) пуст, и рабочий процесс вынужден задерживаться до получения задачи. Кроме того, выполнение од­ной задачи обычно приводит к возникновению двух меньших задач, которые рабочий процесс должен поместить в портфель. Наконец, здесь гораздо труднее определить, когда работа будет завершена, поскольку просто ждать опустошения портфеля недостаточно. (Действительно, как только будет получена первая задача, портфель станет пустым.) Вместо этого можно считать, что работа сделана, если портфель пуст и каждый рабочий процесс ждет получения новой задачи.

В листинге 3.18 показана программа для адаптивной квадратуры, использующая портфель задач. Он представлен очередью и счетчиком. Еще один счетчик отслеживает число простаи­вающих процессов. Вся работа заканчивается, когда значение переменной size равно нулю, а счетчика idle — п. Заметим, что программа содержит несколько неделимых действий. Они нуж­ны для защиты критических секций, в которых происходит доступ к разделяемым переменным. Все неделимые действия, кроме одного, безусловны, поэтому их можно защитить блокировками. Однако оператор await нужно реализовать с помощью более сложного протокола, описанного в разделе 3.2, или более мощного механизма синхронизации типа семафоров или мониторов.



Программа в листинге 3. 18 задает чрезмерное использование портфеля задач. В частности, решая создать две задачи, рабочий процесс помещает их в портфель, затем выполняет цикл и получает оттуда новую задачу (возможно, ту же, которую только что поместил туда). Вместо этого можно заставить рабочий процесс помещать одну задачу в портфель, а другую оставлять себе для выполнения. Когда портфель заполнится до состояния, обеспечивающего сбалансиро­ванную вычислительную загрузку, следовало бы заставить рабочий процесс выполнять задачу полностью, используя последовательную рекурсию, а не помещать новые задачи в портфель.






Содержание раздела

---

---